7 합성곱 신경망(CNN)의 진화

“때로는 가장 단순한 아이디어가 가장 큰 혁신을 가져온다.” - 윌리엄 오컴 (William of Ockham), 철학자

합성곱 신경망(Convolutional Neural Network, CNN)은 1989년 얀 르쿤(Yann LeCun)의 역전파 알고리즘을 이용한 학습 가능한 컨볼루션 필터 연구와, 1998년 LeNet-5의 성공적인 손글씨 숫자 인식으로 그 가능성을 보였습니다. 2012년, AlexNet은 ImageNet Large Scale Visual Recognition Challenge (ILSVRC)에서 압도적인 성능으로 우승하며 딥러닝, 특히 CNN의 시대를 열었습니다. 그러나 AlexNet 이후, 네트워크의 깊이를 늘리는 시도는 기울기 소실/폭주(vanishing/exploding gradients) 문제로 인해 어려움을 겪었습니다.

2015년, 마이크로소프트 연구팀의 Kaiming He 등이 제안한 ResNet(Residual Network)은 “잔차 학습(residual learning)”이라는 획기적인 아이디어를 통해 이 문제를 해결했습니다. ResNet은 이전에는 불가능했던 152층 깊이의 네트워크를 성공적으로 훈련시켰으며, 이미지 인식 분야에서 새로운 기준을 세웠습니다. ResNet의 핵심 요소인 잔차 연결(residual connection)은 현재 대부분의 딥러닝 아키텍처에서 필수적인 요소로 자리 잡았습니다.

본 장에서는 CNN의 탄생 배경과 발전 과정을 살펴보고, ResNet의 핵심 아이디어와 구조, 구현 방법을 심층적으로 분석합니다. 또한, CNN 발전에서 중요한 이정표가 된 Inception 모듈과 EfficientNet의 핵심 개념도 함께 다루어, 현대 CNN 아키텍처의 진화를 폭넓게 이해할 수 있도록 하겠습니다

7.1 컨볼루션 신경망의 탄생

도전 과제: 어떻게 하면 컴퓨터가 이미지 내의 객체를 사람처럼 인식할 수 있을까?

연구자의 고뇌: 초기 컴퓨터 비전 연구자들은 이미지를 픽셀 값의 단순한 집합으로 취급하는 대신, 이미지 내의 특징(feature)을 추출하고 이를 기반으로 객체를 인식하는 방법을 찾고자 했습니다. 하지만 어떤 특징이 중요한지, 그리고 그 특징을 어떻게 효율적으로 추출할 수 있을지는 명확하지 않았습니다.

1960년대 초, David Hubel과 Torsten Wiesel은 고양이의 시각 피질에 대한 실험을 통해, 특정 뉴런들이 특정 시각 패턴(예: 수직선, 수평선, 특정 방향의 경계)에만 선택적으로 반응한다는 것을 발견했습니다. 이들은 이 연구로 1981년 노벨 생리의학상을 수상했지만, 당시에는 이 발견이 훗날 인공지능 분야에 혁명적인 발전을 가져올 것이라고는 누구도 예상하지 못했습니다. Hubel과 Wiesel의 발견은 현대 CNN의 두 가지 핵심 개념인 컨볼루션 레이어(convolutional layer)와 풀링 레이어(pooling layer)의 생물학적 토대가 됩니다.

• 단순 세포 (Simple cells): 특정 방향의 에지(edge)나 선분과 같은 국소적인 특징에 반응합니다. 이는 CNN의 컨볼루션 레이어가 필터(커널)를 사용하여 이미지의 국소적인 특징을 추출하는 방식과 유사합니다.
• 복잡 세포 (Complex cells): 단순 세포의 출력에 대해 위치 불변성(translation invariance)을 가집니다. 즉, 특정 패턴이 이미지의 어느 위치에 나타나든 반응합니다. 이는 CNN의 풀링 레이어가 특징 맵의 크기를 줄이면서도 위치 정보를 어느 정도 유지하는 방식과 유사합니다.

1980년, 후쿠시마 쿠니히코(Kunihiko Fukushima)는 이러한 개념을 바탕으로 CNN의 원형이라고 할 수 있는 네오코그니트론(Neocognitron)을 제안했습니다. 네오코그니트론은 여러 층의 S-cell (simple cell)과 C-cell (complex cell)로 구성되어, 이미지의 계층적인 특징을 추출하고, 위치 변화에 강인한 패턴 인식을 수행할 수 있었습니다.

하지만, 당시의 네오코그니트론은 학습 알고리즘이 정립되지 않아, 필터(가중치)를 수동으로 설정해야 했습니다. 1989년, 얀 르쿤(Yann LeCun)은 오차 역전파(backpropagation) 알고리즘을 컨볼루션 신경망에 적용하여, 필터를 데이터로부터 자동으로 학습할 수 있도록 했습니다. 이로써 현대적인 CNN이 탄생했으며, LeNet-5라는 이름으로 손글씨 숫자 인식에서 뛰어난 성능을 보였습니다.

2012년, AlexNet은 ImageNet 챌린지에서 압도적인 성능으로 우승하며 딥러닝, 특히 CNN의 시대를 열었습니다. AlexNet은 LeNet-5보다 훨씬 더 깊고 복잡한 구조를 가졌으며, GPU를 활용한 병렬 연산을 통해 대규모 데이터셋(ImageNet)을 효율적으로 학습할 수 있었습니다.

7.1.1 디지털 신호 처리의 발전과 CNN의 배경

컴퓨터 비전과 CNN을 깊이 이해하려면, 디지털 신호 처리(Digital Signal Processing, DSP) 분야의 발전 과정을 살펴볼 필요가 있습니다. 1807년, 조제프 푸리에(Joseph Fourier)는 모든 주기 함수를 사인(sin) 함수와 코사인(cos) 함수의 합으로 분해할 수 있다는 푸리에 변환(Fourier Transform)을 제안했습니다. 이는 신호 처리 분야의 초석이 되었으며, 시간 영역(time domain)의 신호를 주파수 영역(frequency domain)으로 변환하여 분석하는 것을 가능하게 했습니다.

특히, 1960년대 디지털 컴퓨터의 발전과 함께 고속 푸리에 변환(Fast Fourier Transform, FFT) 알고리즘이 개발되면서, 디지털 신호 처리는 새로운 전기를 맞이했습니다. FFT는 푸리에 변환을 훨씬 빠르게 계산할 수 있게 해주었고, 이미지, 음성, 통신 등 다양한 분야에서 신호 처리 기술이 널리 사용되기 시작했습니다.

이미지 처리에서 컨볼루션 연산은 핵심적인 역할을 합니다. 컨볼루션은 입력 신호(이미지)에 필터(커널)를 적용하여 원하는 특징을 추출하거나 노이즈를 제거하는 기본적인 연산입니다. 1960년대부터 발전한 디지털 필터 이론은 이미지의 경계 검출(edge detection), 블러링(blurring), 샤프닝(sharpening) 등 다양한 처리를 가능하게 했습니다. 1960년대 후반에는 칼만 필터(Kalman Filter)가 등장하여, 노이즈가 섞인 측정값으로부터 시스템의 상태를 추정하는 강력한 도구를 제공했습니다. 칼만 필터는 베이즈 정리(Bayes’ theorem)에 기반한 재귀적인 알고리즘을 사용하며, 오늘날 컴퓨터 비전의 객체 추적(object tracking), 로봇 비전 등에서 필수적으로 사용됩니다.

이러한 전통적인 디지털 신호 처리 기술들은 CNN의 이론적 기반이 되었습니다. 하지만 기존의 필터들은 사람이 직접 설계해야 했고, 고정된 형태를 가졌기 때문에 다양한 패턴을 인식하는 데 한계가 있었습니다. CNN은 이러한 한계를 극복하고, 데이터로부터 최적의 필터를 자동으로 학습할 수 있도록 함으로써, 이미지 인식 분야에 혁명을 가져왔습니다.

7.1.2 디지털 필터와 컨볼루션

CNN을 이해하기 위해서는 먼저 디지털 필터의 개념을 이해해야 합니다. 디지털 필터는 신호 처리에서 두 가지 주요 목적으로 사용됩니다.

1. 신호 분리 (Signal Separation): 혼합된 신호에서 원하는 신호 성분만 분리합니다. (예: 태아의 심장 박동과 산모의 심장 박동이 섞여 있을 때, 태아의 심장 박동만 분리)
2. 신호 복원 (Signal Restoration): 왜곡되거나 손상된 신호를 원래의 신호에 가깝게 복원합니다. (예: 이미지의 노이즈 제거, 흐릿한 이미지 복원)

가장 기본적인 디지털 필터 중 하나는 Sobel 필터입니다. Sobel 필터는 3x3 크기의 행렬로, 이미지의 경계(edge)를 검출하는 데 사용됩니다.

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

import numpy as np
# Sobel filter for vertical edge detection
sobel_vertical = np.array([
    [-1, 0, 1],
    [-2, 0, 2],
    [-1, 0, 1]
])

# Sobel filter for horizontal edge detection
sobel_horizontal = np.array([
    [-1, -2, -1],
    [ 0,  0,  0],
    [ 1,  2,  1]
])

먼저 고전적 디지털 필터가 어떤 작용을 하는지 살펴보겠습니다. 전체 코드는 chapter_06/filter_utils.py에 있습니다.

import matplotlib.pyplot as plt
from dldna.chapter_07.filter_utils import show_filter_effects, create_convolution_animation
%matplotlib inline

# 테스트용 이미지 URL
IMAGE_URL = "https://raw.githubusercontent.com/opencv/opencv/master/samples/data/building.jpg"

# 필터 효과 시각화
show_filter_effects(IMAGE_URL)

위 예제는 다음과 같은 필터가 사용되었습니다.

filters = {
    'Gaussian Blur': cv2.getGaussianKernel(3, 1) @ cv2.getGaussianKernel(3, 1).T,
    'Sharpen': np.array([
        [0, -1, 0],
        [-1, 5, -1],
        [0, -1, 0]
    ]),
    'Edge Detection': np.array([
        [-1, -1, -1],
        [-1, 8, -1],
        [-1, -1, -1]
    ]),
    'Emboss': np.array([
        [-2, -1, 0],
        [-1, 1, 1],
        [0, 1, 2]
    ]),
    'Sobel X': np.array([
        [-1, 0, 1],
        [-2, 0, 2],
        [-1, 0, 1]
    ])
}

이 필터들이 작동하는 방식이 바로 컨볼루션입니다. 필터를 이미지 위에서 슬라이딩(sliding)하면서 각 위치에서 필터와 이미지 부분의 요소별 곱(element-wise multiplication)의 합을 계산합니다. 이는 다음 수식으로 표현할 수 있습니다.

\((I * K)(x, y) = \sum_{i=-a}^{a}\sum_{j=-b}^{b} I(x+i, y+j)K(i, j)\)

여기서 \(I\)는 입력 이미지, \(K\)는 커널(필터)입니다. \((x,y)\)는 출력 픽셀의 좌표, \((i,j)\)는 커널 내부의 좌표, \(a\)와 \(b\)는 각각 커널의 가로/세로 절반 크기입니다.

컨볼루션 연산은 시각적으로 이해하면 더 쉽습니다. 아래는 컨볼루션 연산 과정을 보여주는 애니메이션입니다.

from dldna.chapter_07.conv_visual import create_conv_animation
from IPython.display import HTML
%matplotlib inline

# 애니메이션 생성 및 표시
animation = create_conv_animation()

# js_html = animation.to_jshtml()
# display(HTML(f'<div style="width:700px">{js_html}</div>'))

# html_video = animation.to_html5_video()
# display(HTML(f'<div style="width:700px">{html_video}</div>'))

display(animation)

Once Loop Reflect

디지털 필터의 가장 큰 한계는 고정된 특성에 있습니다. Sobel, Gaussian과 같은 전통적인 필터들은 특정 패턴만을 검출하도록 수동 설계되어 있어 복잡하고 다양한 패턴을 인식하는 데 한계가 있습니다. 또한 이미지의 크기나 회전 변화에 취약하고 여러 계층의 특징을 자동 학습할 수 없다는 단점이 있습니다. 이러한 한계는 데이터 기반의 학습 가능한 필터인 CNN의 발전으로 이어졌습니다.

7.1.2 CNN의 특징과 구조

CNN은 생물학적 시각 처리 메커니즘을 모방하여 이미지 내의 공간적 계층 구조(spatial hierarchy)를 효율적으로 학습합니다.

학습 가능한 필터 (Learnable Filters)

CNN의 가장 큰 특징은 기존의 수동으로 설계된 필터(예: Sobel, Gabor 필터) 대신, 데이터로부터 자동으로 학습되는 필터를 사용한다는 점입니다. 이는 CNN이 특정 작업(예: 이미지 분류, 객체 검출)에 최적화된 특징 추출기를 스스로 학습할 수 있게 해줍니다.

import torch
import torch.nn as nn
import torch.nn.functional as F

class SimpleCNN(nn.Module):
    def __init__(self):
        super().__init__()
        # Multiple learnable filters: 32 (channels) of 3x3 filter weight matrices + 32 biases
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3, padding=1)
        # Multiple learnable filters: For 32 input channels, 64 output channels of 3x3 filter weight matrices + 64 biases
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        return x

위 SimpleCNN 예제에서 conv1과 conv2는 각각 학습 가능한 필터를 가진 컨볼루션 레이어입니다. nn.Conv2d의 첫 번째 인자는 입력 채널 수, 두 번째 인자는 출력 채널 수(필터의 개수), kernel_size는 필터의 크기, padding은 입력 이미지 주변에 0을 채워 넣어 출력 특징 맵의 크기를 조절하는 역할을 합니다.

계층적 특징 추출 (Hierarchical Feature Extraction)

CNN은 여러 층의 컨볼루션과 풀링 연산을 통해 이미지의 계층적인 특징을 추출합니다.

• 초기 층 (Low-level features): 에지(edge), 선(line), 색상 변화와 같은 기본적인 시각적 특징(저수준 특징)을 감지합니다.
• 중간 층 (Mid-level features): 텍스처(texture), 패턴, 간단한 모양과 같은 중간 수준의 특징을 학습합니다.
• 마지막 층 (High-level features): 객체의 부분, 객체의 전체적인 구조와 같은 추상적이고 고수준의 특징을 인식합니다.

이러한 계층적 특징 추출은 인간의 시각 시스템이 시각 정보를 단계적으로 처리하는 방식과 유사합니다.

import torch
import torch.nn as nn
import torch.nn.functional as F

class HierarchicalCNN(nn.Module):
    def __init__(self):
        super().__init__()
        # Low-level feature extraction
        self.conv1 = nn.Conv2d(3, 64, 3, padding=1)
        self.bn1 = nn.BatchNorm2d(64)

        # Mid-level feature extraction
        self.conv2 = nn.Conv2d(64, 128, 3, padding=1)
        self.bn2 = nn.BatchNorm2d(128)

        # High-level feature extraction
        self.conv3 = nn.Conv2d(128, 256, 3, padding=1)
        self.bn3 = nn.BatchNorm2d(256)

    def forward(self, x):
        # Low-level features (edges, textures)
        x = F.relu(self.bn1(self.conv1(x)))

        # Mid-level features (patterns, partial shapes)
        x = F.relu(self.bn2(self.conv2(x)))

        # High-level features (object parts, overall structure)
        x = F.relu(self.bn3(self.conv3(x)))
        return x

위 HierarchicalCNN 예제는 3개의 컨볼루션 층을 사용하여 저수준, 중간 수준, 고수준 특징을 추출하는 CNN을 보여줍니다. 실제로는 이보다 훨씬 더 많은 층을 쌓아 더 복잡한 특징을 학습합니다.

공간적 계층 구조 (Spatial Hierarchy) 및 풀링(Pooling)

CNN의 각 층은 일반적으로 컨볼루션 연산, 활성화 함수(ReLU 등), 풀링 연산으로 구성됩니다.

• 컨볼루션 층: 필터를 사용하여 입력 특징 맵에서 특징을 추출합니다.
• 활성화 함수: ReLU와 같은 비선형 함수를 적용하여 네트워크에 비선형성을 추가합니다.
• 풀링 층: 특징 맵의 크기를 줄여 (downsampling) 계산량을 감소시키고, 위치 불변성(translation invariance)을 강화합니다. 즉, 객체가 이미지 내에서 약간 이동하더라도 동일한 객체로 인식할 수 있도록 합니다. 일반적으로 최대 풀링(max pooling)이 사용됩니다.

이러한 구조적 특성 덕분에 CNN은 이미지의 공간적 정보를 효과적으로 학습하고, 이미지 내 객체의 위치 변화에 강인한(robust) 특징을 추출할 수 있습니다.

파라미터 공유 (Parameter Sharing)

파라미터 공유는 CNN의 핵심적인 효율성 메커니즘입니다. 동일한 필터가 입력 이미지(또는 특징 맵)의 모든 위치에서 사용됩니다. 이는 각 위치에서 동일한 특징을 탐지한다는 가정을 바탕으로 합니다. (예: 수직선 필터는 이미지의 왼쪽 위나 오른쪽 아래나 동일하게 수직선을 검출)

1. 메모리 효율성: 필터의 파라미터가 모든 위치에서 공유되므로, 모델의 파라미터 수가 획기적으로 감소합니다. 예를 들어, 32x32 컬러(3 채널) 이미지에 3x3 크기의 필터 64개를 적용하는 컨볼루션 레이어가 있을 때, 각 필터는 3x3x3 = 27개의 파라미터를 가집니다. 만약 파라미터 공유를 하지 않는다면, 32x32 위치마다 다른 필터를 사용해야 하므로, 총 (32x32) x (3x3x3) x 64 개의 파라미터가 필요합니다. 하지만 파라미터 공유를 사용하면, 27 x 64 + 64(편향) = 1792개의 파라미터만 필요합니다.

2. 통계적 효율성: 동일한 필터가 이미지의 여러 위치에서 특징을 학습하므로, 더 적은 수의 파라미터로도 효과적인 특징 추출기를 학습할 수 있습니다. 이는 모델의 일반화 성능을 향상시킵니다.

3. 병렬처리: 컨볼루션 연산은 각 필터가 독립적으로 적용된 후 그 결과를 합하는 것이기 때문에 병렬처리에 매우 용이합니다.

from dldna.chapter_07.param_share import compare_parameter_counts, show_example

# 다양한 입력 크기에 따른 비교. CNN 입출력 채널을 1로 고정.
input_sizes = [8, 16, 32, 64, 128]
comparison = compare_parameter_counts(input_sizes)
print("\nParameter Count Comparison:")
print(comparison)

# 32x32 입력에 대한 상세 예시
show_example(32)

Parameter Count Comparison:
  Input Size  Conv Params  FC Params  Ratio (FC/Conv)
0        8x8           10       4160            416.0
1      16x16           10      65792           6579.2
2      32x32           10    1049600         104960.0
3      64x64           10   16781312        1678131.2
4    128x128           10  268451840       26845184.0

Example with 32x32 input:
CNN parameters: 10 (fixed)
FC parameters: 1,049,600
Parameter reduction: 99.9990%

수용 영역 (Receptive Field)

수용 영역(receptive field)은 특정 뉴런의 출력에 영향을 미치는 입력 이미지 영역의 크기를 의미합니다. CNN에서 컨볼루션 층과 풀링 층을 거치면서 수용 영역은 점진적으로 커집니다.

• 초기 층: 작은 수용 영역을 가지므로, 지역적인(local) 특징(예: 에지, 점)을 감지합니다.
• 깊은 층: 넓은 수용 영역을 가지므로, 더 넓은 문맥(context)을 고려하여 추상적인(abstract) 특징(예: 객체의 부분, 객체 전체)을 학습합니다.

이러한 계층적 특징 추출과 넓어지는 수용 영역 덕분에 CNN은 이미지 인식에서 뛰어난 성능을 보일 수 있습니다.

결론적으로, CNN은 생물학적 시각 처리 시스템에서 영감을 받아, 컨볼루션 연산, 풀링 연산, 학습 가능한 필터, 파라미터 공유, 계층적 특징 추출 등의 핵심적인 특징들을 통해 이미지 인식 및 컴퓨터 비전 분야에서 혁신적인 발전을 이끌었습니다.

7.1.3 CNN의 수학적 표현과 구현

CNN의 수학 표현은 다음과 같습니다.

\((F * K)(p) = \sum_{s+t=p} F(s)K(t) = \sum_{i}\sum_{j} F(i,j)K(p_x-i, p_y-j)\)

여기서 F는 입력 특징 맵, K는 커널을 나타냅니다. 실제 구현에서는 다중 채널과 배치 처리를 고려해야 하므로 다음과 같이 확장됩니다.

\(Y_{n,c_{out},h,w} = \sum_{c_{in}}\sum_{i=0}^{k_h-1}\sum_{j=0}^{k_w-1} X_{n,c_{in},h+i,w+j} \cdot W_{c_{out},c_{in},i,j} + b_{c_{out}}\)

여기서: - \(n\)은 배치 인덱스 - \(c_{in}\), \(c_{out}\)은 입력/출력 채널 - \(h\), \(w\)는 높이와 너비 - \(k_h\), \(k_w\)는 커널 크기 - \(W\)는 가중치, \(b\)는 편향

2d 컨볼루션과 맥스풀링을 pytorch 소스코드를 참조해서 학습용으로 구현한 클래스가 chapter_06/simple_conv.py입니다. 교육용 목적으로 CUDA 최적화없이 for 루프를 사용하고 예외처리 등도 없앴습니다. 소스 코드에 상세한 주석이 있으므로 클래스에 대한 설명은 생략하도록 하겠습니다.

import torch
import matplotlib.pyplot as plt
from dldna.chapter_07.simple_conv import SimpleConv2d, SimpleMaxPool2d
# %matplotlib inline  # This line is only needed in Jupyter/IPython environments

# Input data creation (e.g., 1 image, 1 channel, 6x6 size)
x = torch.tensor([
    [1, 2, 3, 4, 5, 6],
    [7, 8, 9, 10, 11, 12],
    [13, 14, 15, 16, 17, 18],
    [19, 20, 21, 22, 23, 24],
    [25, 26, 27, 28, 29, 30],
    [31, 32, 33, 34, 35, 36]
], dtype=torch.float32).reshape(1, 1, 6, 6)

# SimpleConv2d test
conv = SimpleConv2d(in_channels=1, out_channels=2, kernel_size=3, padding=1)
conv_output = conv(x)

# SimpleMaxPool2d test
pool = SimpleMaxPool2d(kernel_size=2)
pool_output = pool(x)

# Visualize results
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Original image
axes[0].imshow(x[0, 0].detach().numpy(), cmap='viridis')
axes[0].set_title('Original Image')

# Convolution result (first channel)
axes[1].imshow(conv_output[0, 0].detach().numpy(), cmap='viridis')
axes[1].set_title('Conv2d Output (Channel 0)')

# Pooling result
axes[2].imshow(pool_output[0, 0].detach().numpy(), cmap='viridis')
axes[2].set_title('MaxPool2d Output')

for ax in axes:
    ax.axis('off')
plt.tight_layout()
plt.show()

# Print output sizes
print("Input size:", x.shape)
print("Convolution output size:", conv_output.shape)
print("Pooling output size:", pool_output.shape)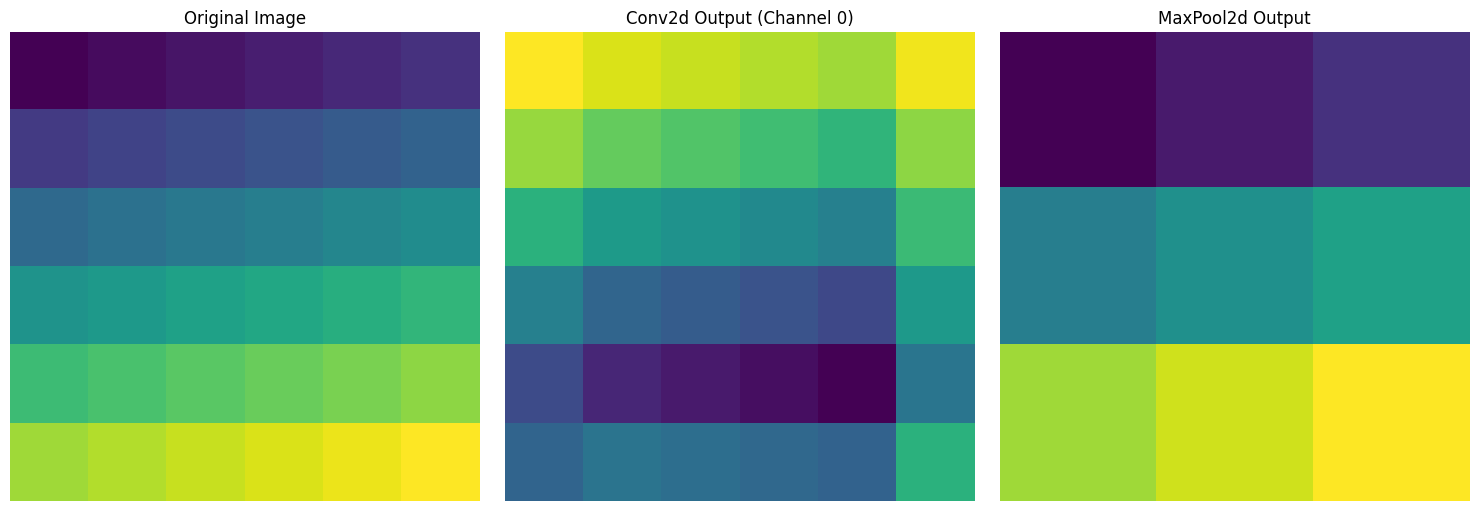

Input size: torch.Size([1, 1, 6, 6])
Convolution output size: torch.Size([1, 2, 6, 6])
Pooling output size: torch.Size([1, 1, 3, 3])

6x6 크기의 입력 이미지에 대해 세 가지 결과를 시각화했습니다. 왼쪽은 1부터 36까지 순차적으로 증가하는 원본 이미지, 중앙은 3x3 컨볼루션 필터를 적용한 결과, 오른쪽은 2x2 최대 풀링을 적용하여 크기가 절반으로 줄어든 결과를 보여줍니다.

클릭하여 내용 보기 (딥다이브: 컨볼루션 연산의 주파수 영역 해석과 1x1 컨볼루션의 의미)

컨볼루션 연산의 주파수 영역 해석과 1x1 컨볼루션의 의미

CNN의 핵심 연산인 컨볼루션을 주파수 영역에서 해석하고, 특히 1x1 컨볼루션의 의미를 깊이 있게 탐구합니다. 푸리에 변환과 컨볼루션 정리를 통해 컨볼루션 연산의 숨겨진 의미를 파헤쳐 보겠습니다.

1. 컨볼루션 연산 복습

7.1.2절과 7.1.3절에서 다룬 컨볼루션 연산을 간략히 복습합니다. 2차원 이미지 \(I\)와 커널(필터) \(K\)의 컨볼루션 연산 \(I * K\)는 다음과 같이 정의됩니다.

\((I * K)[i, j] = \sum_{m} \sum_{n} I[i-m, j-n] K[m, n]\)

여기서 \(i\), \(j\)는 출력 이미지의 픽셀 위치, \(m\), \(n\)은 커널의 픽셀 위치입니다. 이산 컨볼루션(discrete convolution)은 커널을 이미지 위에서 슬라이딩하면서, 겹치는 영역의 원소별 곱셈 후 합산을 수행하는 과정입니다.

2. 푸리에 변환 (Fourier Transform) 소개

푸리에 변환은 시간 영역(spatial domain)의 신호를 주파수 영역(frequency domain)으로 변환하는 강력한 도구입니다.

• 시간 영역 vs. 주파수 영역: 시간 영역은 우리가 일반적으로 인식하는 신호의 형태입니다 (예: 시간에 따른 이미지의 픽셀 값 변화). 주파수 영역은 신호가 어떤 주파수 성분들로 구성되어 있는지를 나타냅니다 (예: 이미지에 포함된 다양한 공간 주파수 성분).

• 푸리에 변환의 정의: 푸리에 변환은 신호를 다양한 주파수와 진폭을 갖는 사인(sine) 및 코사인(cosine) 함수의 합으로 분해합니다. 연속 함수 \(f(t)\)의 푸리에 변환 \(\mathcal{F}\{f(t)\} = F(\omega)\)는 다음과 같이 정의됩니다.

  \(F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt\)

  여기서 \(j\)는 허수 단위, \(\omega\)는 각주파수(angular frequency)입니다. 역 푸리에 변환(Inverse Fourier Transform)은 주파수 영역의 신호를 다시 시간 영역으로 복원합니다.

  \(f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{j\omega t} d\omega\)

• 이산 푸리에 변환 (DFT) & 고속 푸리에 변환 (FFT): 컴퓨터는 연속적인 신호를 다룰 수 없으므로, 이산 푸리에 변환(Discrete Fourier Transform, DFT)을 사용합니다. DFT는 이산적인 데이터에 대해 푸리에 변환을 수행합니다. 고속 푸리에 변환(Fast Fourier Transform, FFT)은 DFT를 효율적으로 계산하는 알고리즘입니다. DFT의 수식은 다음과 같습니다.

\(X[k] = \sum_{n=0}^{N-1} x[n] e^{-j(2\pi/N)kn}\), \(k = 0, 1, ..., N-1\)

여기서 \(x[n]\)은 이산 신호, \(X[k]\)는 DFT 결과, \(N\)은 신호의 길이입니다.

3. 컨볼루션 정리 (Convolution Theorem)

컨볼루션 정리는 컨볼루션 연산과 푸리에 변환 사이의 중요한 관계를 설명합니다. 핵심은 시간 영역에서의 컨볼루션이 주파수 영역에서는 단순한 곱셈으로 변환된다는 것입니다.

• 컨볼루션 정리: 두 함수 \(f(t)\)와 \(g(t)\)의 컨볼루션 \(f(t) * g(t)\)의 푸리에 변환은 각 함수의 푸리에 변환의 곱과 같습니다.

  \(\mathcal{F}\{f * g\} = \mathcal{F}\{f\} \cdot \mathcal{F}\{g\}\)

  즉, \(F(\omega)\)와 \(G(\omega)\)가 각각 \(f(t)\)와 \(g(t)\)의 푸리에 변환이라면, \(f(t) * g(t)\)의 푸리에 변환은 \(F(\omega)G(\omega)\)입니다.

• 주파수 영역에서의 해석: 컨볼루션 정리는 컨볼루션 연산을 주파수 영역에서 해석할 수 있게 해줍니다. 컨볼루션 필터는 입력 신호의 특정 주파수 성분을 강조하거나 억제하는 역할을 합니다. 주파수 영역에서 곱셈은 해당 주파수 성분의 진폭을 조절하는 것과 같습니다.

4. 컨볼루션 필터의 주파수 응답 (Frequency Response)

다양한 컨볼루션 필터의 주파수 응답을 분석하면, 필터가 어떤 주파수 성분을 통과시키고 어떤 성분을 차단하는지 알 수 있습니다.

• 주파수 응답 시각화: 필터의 푸리에 변환을 계산하여 주파수 응답을 얻을 수 있습니다. 주파수 응답은 일반적으로 크기(magnitude)와 위상(phase)으로 표현됩니다. 크기는 각 주파수 성분의 진폭 변화를, 위상은 위상 변화를 나타냅니다.

• 필터 유형:

  • Low-pass filter (저주파 통과 필터): 저주파 성분은 통과시키고 고주파 성분은 차단합니다. 이미지를 흐릿하게(blurring) 만드는 효과가 있습니다 (예: Gaussian filter).
  • High-pass filter (고주파 통과 필터): 고주파 성분은 통과시키고 저주파 성분은 차단합니다. 이미지의 경계(edge)를 강조하는 효과가 있습니다 (예: Sobel filter).
  • Band-pass filter (대역 통과 필터): 특정 주파수 대역만 통과시키고 나머지는 차단합니다.

  아래는 Sobel 필터와 Gaussian 필터의 주파수 응답을 시각화한 예시입니다. (코드를 실행하면 이미지가 생성됩니다.)

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d

def plot_frequency_response(kernel, title):
    # Calculate the 2D FFT of the kernel
    kernel_fft = np.fft.fft2(kernel, s=(256, 256)) # Zero-padding for better visualization
    kernel_fft_shifted = np.fft.fftshift(kernel_fft) # Shift zero frequency to center

    # Calculate the magnitude and phase
    magnitude = np.abs(kernel_fft_shifted)
    phase = np.angle(kernel_fft_shifted)

    # Plot the magnitude response
    plt.figure(figsize=(12, 6))
    plt.subplot(1, 2, 1)
    plt.imshow(np.log(1 + magnitude), cmap='gray') # Log scale for better visualization
    plt.title(f'{title} - Magnitude Response')
    plt.colorbar()
    plt.axis('off')


    #Plot the phase response
    plt.subplot(1, 2, 2)
    plt.imshow(phase, cmap='hsv')
    plt.title(f'{title} - Phase Response')
    plt.colorbar()
    plt.axis('off')
    plt.show()



# Example kernels
sobel_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
gaussian = np.array([[1, 4, 6, 4, 1],
                      [4, 16, 24, 16, 4],
                      [6, 24, 36, 24, 6],
                      [4, 16, 24, 16, 4],
                      [1, 4, 6, 4, 1]]) / 256.0

# Plot frequency responses
plot_frequency_response(sobel_x, 'Sobel X Filter')
plot_frequency_response(sobel_y, 'Sobel Y Filter')
plot_frequency_response(gaussian, 'Gaussian Filter')

5. 1x1 컨볼루션의 주파수 영역 해석

1x1 컨볼루션은 공간적인 정보는 그대로 유지하면서 채널 간의 연산을 수행합니다.

• 채널 간 선형 조합: 1x1 컨볼루션은 각 픽셀 위치에서 채널들을 선형 조합합니다. 이는 주파수 영역에서 각 채널의 주파수 성분에 대한 가중합으로 해석할 수 있습니다. 즉, 1x1 컨볼루션 필터의 가중치는 각 채널의 주파수 성분에 대한 중요도를 나타냅니다.

• 상관 관계 조절 및 특징 재구성: 1x1 컨볼루션은 채널 간의 상관 관계(correlation)를 조절합니다. 강한 상관 관계를 갖는 채널들을 결합하거나, 불필요한 채널을 제거하여 특징 표현을 재구성합니다.

• Inception 모듈에서의 역할: Inception 모듈에서 1x1 컨볼루션은 두 가지 중요한 역할을 합니다.

  • 차원 축소: 채널 수를 줄여 계산량을 감소시킵니다.
  • 비선형성 추가: 1x1 컨볼루션 후 ReLU와 같은 비선형 활성화 함수를 적용하여 모델의 표현력을 높입니다. 주파수 응답관점에서 보면 서로 다른 주파수 응답을 가지는 채널들을 섞어 더 복잡한 주파수 응답을 만들어 낼 수 있게 합니다.

7.1.4 CNN의 학습 가능한 파라미터 계산

CNN의 학습 가능한 파라미터 수를 계산하는 것은 네트워크 설계와 최적화에 매우 중요합니다. 단계별로 살펴보겠습니다.

1. 기본 컨볼루션 레이어

conv = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3)

파라미터 계산은 다음과 같습니다. - 각 필터 크기: 3 × 3 × 1 (커널크기² × 입력채널) - 필터 개수: 32 (출력채널) - 편향(bias): 32 (출력채널과 동일) - 총 파라미터 = (3 × 3 × 1) × 32 + 32 = 320

2. 최대 풀링 레이어

maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

• 학습 가능한 파라미터 없음
• 단순히 2×2 영역에서 최대값을 선택하는 연산만 수행
• 특징 맵의 크기만 줄어듦 (높이와 너비가 각각 1/2로)

3. 패딩이 있는 컨볼루션

conv = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1)

패딩은 출력 크기에만 영향을 주고 파라미터 수는 변하지 않는다. - 각 필터 크기: 3 × 3 × 3 - 필터 개수: 64 - 총 파라미터 = (3 × 3 × 3) × 64 + 64 = 1,792

4. 스트라이드가 있는 컨볼루션과 풀링의 조합

conv = nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=2)
maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

• 컨볼루션 파라미터 = (3 × 3 × 64) × 128 + 128 = 73,856
• 풀링 파라미터 = 0
• 총 파라미터 = 73,856

출력 크기 계산.

컨볼루션 출력크기 = ((입력크기 + 2×패딩 - 커널크기) / 스트라이드) + 1
풀링 출력크기 = ((입력크기 - 풀링크기) / 풀링스트라이드) + 1

5. 복잡한 구조의 예 (ResNet 기본 블록)

class BasicBlock(nn.Module):
    def __init__(self, in_channels=64, out_channels=64):
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

파라미터 계산. 1. 첫 번째 컨볼루션: (3 × 3 × 64) × 64 + 64 = 36,928 2. 첫 번째 배치 정규화: 64 × 2 = 128 (감마와 베타) 3. 두 번째 컨볼루션: (3 × 3 × 64) × 64 + 64 = 36,928 4. 두 번째 배치 정규화: 64 × 2 = 128 5. 최대 풀링: 0

총 파라미터 = 74,112

이러한 파라미터 개수 계산은 모델의 복잡도를 이해하고, 메모리 요구사항을 예측하며, 과적합 위험을 평가하는 데 매우 중요합니다. 특히 풀링 레이어는 파라미터 없이도 특징 맵의 크기를 효과적으로 줄여주어 계산 효율성을 높이는 데 큰 도움을 줍니다.

7.1.5 CNN: 특징 추출과 추상화의 학습

CNN의 핵심은 “학습 가능한 필터”를 통해 이미지의 특징을 추출하고, 이를 계층적으로 조합하여 더 추상적인 표현을 학습하는 데 있습니다. 이 과정은 이미지의 구체적인 디테일에서 시작하여, 추상적인 의미(예: 객체의 종류)를 파악하는 단계로 진행되며, 다음 두 가지 주요 측면으로 나누어 볼 수 있습니다.

1. 이미지 특징의 추출과 변환 (Feature Extraction and Transformation): 이미지의 국소 영역에서 특징을 추출하고, 비선형 활성화 함수를 통해 유의미한 특징만 남깁니다.
2. 필터(채널) 수 증가와 추상화 공간의 확장 (Increasing Filters and Expanding Abstract Space): 층이 깊어질수록 필터(채널) 수를 늘려, 더 다양하고 추상적인 특징을 학습합니다.

1. 이미지 특징의 추출과 변환

CNN의 컨볼루션 층은 입력 이미지(또는 이전 층의 특징 맵)에 대해 학습 가능한 필터를 적용하여 특징을 추출합니다. 각 필터는 이미지의 특정 패턴(예: 에지, 텍스처, 모양)에 반응하도록 학습됩니다. 이 과정은 다음 단계로 이루어집니다.

• 컨볼루션 연산: 필터는 이미지의 국소 영역(receptive field)과 상호 작용하여 해당 영역에 특정 패턴이 있는지 여부를 나타내는 값을 출력합니다. 이 과정을 통해, 이미지의 각 위치에서 필터가 검출하고자 하는 패턴의 강도를 나타내는 특징 맵(feature map)이 생성됩니다.
• 활성화 함수: 컨볼루션 연산의 결과(특징 맵)는 ReLU와 같은 비선형 활성화 함수를 통과합니다. 활성화 함수는 특정 임계값 이상의 값을 갖는 특징만 다음 층으로 전달하고, 그렇지 않은 특징은 무시합니다. 이는 네트워크가 중요한 특징에 집중하고, 불필요한 정보는 제거하도록 돕습니다. (Sparse Representation)
• 풀링 (선택적): 풀링 층은 특징 맵의 크기를 줄이면서(downsampling), 위치 불변성(translation invariance)을 강화합니다. 예를 들어, 최대 풀링(max pooling)은 특정 영역(예: 2x2) 내에서 가장 큰 값을 갖는 특징만 남기고 나머지는 버립니다.

이러한 과정을 거쳐, CNN의 각 컨볼루션 층은 입력 이미지를 특징의 공간으로 변환합니다. 이 특징 공간은 원래의 픽셀 공간보다 추상적이며, 분류나 객체 검출과 같은 작업에 더 유용한 정보를 담고 있습니다.

2. 필터(채널) 수 증가와 추상화 공간의 확장

CNN은 여러 층의 컨볼루션과 풀링 연산을 쌓아 올린 깊은(deep) 구조를 가집니다. 각 층을 통과하면서, 특징 맵의 공간적 크기(spatial dimension: 가로, 세로)는 일반적으로 감소하는 반면, 필터의 수(채널의 수)는 증가합니다. 이는 CNN이 추상화(abstraction)를 학습하는 핵심 메커니즘입니다.

• 공간적 크기 감소: 컨볼루션(stride > 1) 또는 풀링 연산은 특징 맵의 공간적 크기를 줄입니다. 이는 계산량을 감소시키고, 위치 불변성을 강화하는 효과가 있습니다. 즉, 객체가 이미지 내에서 약간 이동하더라도 동일한 객체로 인식할 수 있게 합니다.
• 채널 수 증가: 각 컨볼루션 층은 여러 개의 필터를 사용하여 입력 특징 맵의 다양한 측면을 포착합니다.
  • 초기 층: 에지, 색상 변화와 같은 저수준 특징을 감지합니다. 이러한 저수준 특징은 이미지의 기본적인 구성 요소를 나타냅니다.
  • 중간 층: 초기 층에서 추출된 저수준 특징들을 조합하여 텍스처, 패턴, 간단한 모양과 같은 중간 수준 특징을 감지합니다.
  • 깊은 층: 이전 층에서 추출된 특징들을 조합하여 객체의 부분(눈, 코, 입 등), 더 나아가 객체 자체(사람, 자동차, 동물 등)와 같은 고수준, 추상적인 특징을 감지합니다.

필터(채널) 수의 증가는 CNN이 이미지를 표현하는 데 사용하는 특징의 차원이 증가한다는 것을 의미합니다. 초기 층에서는 이미지의 구체적인 디테일에 집중하는 반면, 깊은 층에서는 이미지의 추상적인 의미를 파악하는 데 필요한 정보를 학습합니다. 이는 마치 인간이 사물을 볼 때, 처음에는 세부적인 부분에 주목하다가 점차 전체적인 형태와 의미를 파악하는 과정과 유사합니다.

CNN 층 구조의 대표적인 예시 (VGGNet):

다음은 VGGNet 아키텍처를 보여주는 그림입니다. VGGNet은 CNN의 깊이가 성능에 미치는 영향을 체계적으로 연구한 대표적인 모델입니다.

• VGGNet Architecture:

VGG16 아키텍처.
출처: K. Simonyan, A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” arXiv:1409.1556, 2014.

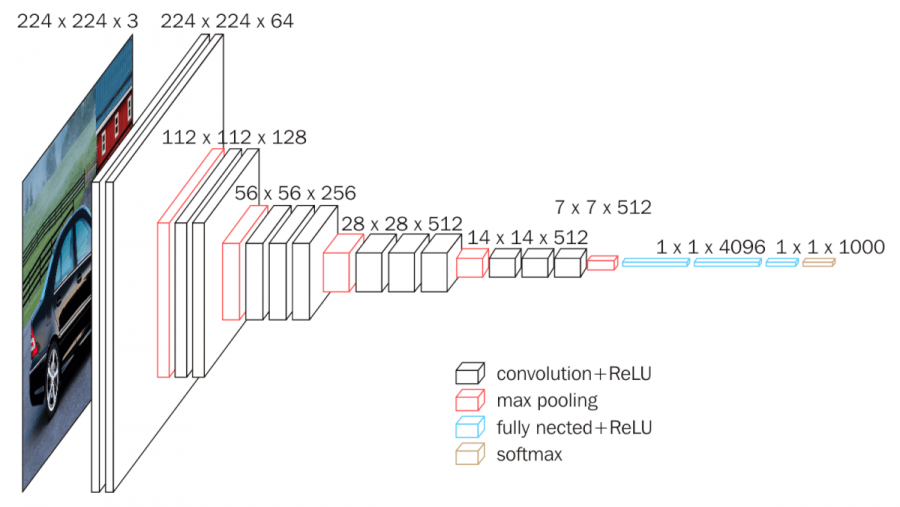
그림에서 볼 수 있듯이, VGGNet은 여러 개의 컨볼루션 층과 풀링 층을 쌓아 올린 구조를 가집니다. 각 층을 통과하면서 특징 맵의 공간적 크기는 감소하고, 채널 수는 증가하는 것을 확인할 수 있습니다. 이는 CNN이 이미지를 저차원의 구체적인 표현(픽셀 값)에서 고차원의 추상적인 표현(객체의 종류)으로 변환하는 과정을 시각적으로 보여줍니다.

결론적으로, CNN의 “학습 가능한 필터”는 이미지의 특징을 추출하고, 이를 계층적으로 조합하여 더 추상적인 표현을 학습하는 강력한 도구입니다. CNN은 여러 층의 컨볼루션과 풀링 연산을 통해 이미지를 더 작고, 더 깊고, 더 추상적인 표현으로 변환하며, 이 과정에서 데이터로부터 이미지의 의미를 파악하는 데 필요한 핵심 정보를 학습합니다. 이러한 특징 추출과 추상화 능력은 CNN이 이미지 인식, 객체 검출, 이미지 분할 등 다양한 컴퓨터 비전 작업에서 뛰어난 성능을 발휘하는 핵심적인 이유입니다.

클릭하여 내용 보기 (딥 다이브 : 딥러닝과 머신러닝에서 ‘커널’ 용어의 다양한 의미)

딥러닝과 머신러닝에서 “커널” 용어의 다양한 의미

“단어는 그 자체로 의미를 가지는 것이 아니라, 맥락 속에서 의미를 가진다.” - (의미론/화용론의 기본 원칙)

딥러닝, 머신러닝, 그리고 신호 처리 분야를 공부하다 보면 “커널(kernel)”이라는 용어를 자주 접하게 됩니다. “커널”은 문맥에 따라 전혀 다른 의미로 사용되기 때문에, 처음 접하는 사람들에게는 혼란을 야기할 수 있습니다. 이 딥다이브에서는 “커널”이 사용되는 다양한 맥락과 그 의미를 명확히 정리하고, 각 용례 간의 연관성을 살펴보겠습니다.

1. 컨볼루션 신경망 (CNN)에서의 커널 (Convolution Kernel)

CNN에서 커널은 필터(filter)와 동의어로 사용됩니다. 컨볼루션 층(convolutional layer)에서 입력 데이터(이미지 또는 특징 맵)에 대해 컨볼루션 연산을 수행하는 작은 크기의 행렬입니다.

• 역할: 이미지의 국소 영역(receptive field)에 대해 특징을 추출합니다.

• 동작 방식: 커널은 입력 데이터 위를 이동(stride)하면서, 겹쳐지는 영역의 픽셀 값과 커널의 가중치를 곱한 후, 그 값들을 모두 더합니다(합성곱 연산). 이 과정을 통해, 커널이 검출하고자 하는 패턴(예: 에지, 텍스처)이 해당 위치에 얼마나 강하게 나타나는지를 나타내는 하나의 값을 출력합니다.

• 학습 가능: CNN에서 커널의 가중치는 역전파(backpropagation) 알고리즘을 통해 데이터로부터 학습됩니다. 즉, CNN은 주어진 문제(예: 이미지 분류)를 해결하는 데 가장 유용한 특징을 추출하도록 커널을 스스로 조정합니다.

• 예시: Sobel 커널

  $

  \[\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix}\]

  $ 이 3x3 크기의 Sobel 커널은 이미지의 수직 경계(vertical edge)를 검출하는 데 사용됩니다.

• 핵심: CNN에서의 커널은 학습 가능한 파라미터를 가지며, 이미지의 국소적인 특징을 추출하는 역할을 합니다.

2. 서포트 벡터 머신 (SVM)에서의 커널 (Kernel Function, Kernel Trick)

SVM(Support Vector Machine)에서 커널은 두 데이터 포인트 사이의 유사도를 계산하는 함수입니다. SVM은 데이터를 고차원 특징 공간(feature space)으로 매핑(mapping)하여, 비선형 분류 문제를 해결합니다. 커널 트릭(kernel trick)은 이 고차원 매핑을 명시적으로 계산하지 않고, 커널 함수를 사용하여 고차원 공간에서의 내적(inner product)을 암묵적으로 계산하는 기법입니다.

• 역할: 데이터를 고차원 특징 공간으로 매핑하여, 비선형 분류 문제를 선형 분류 문제로 변환합니다.
• 핵심: 고차원 특징 공간에서의 내적을 효율적으로 계산합니다. (명시적인 매핑 없이)
• 수학적 표현: \(K(\mathbf{x}, \mathbf{y}) = \phi(\mathbf{x}) \cdot \phi(\mathbf{y})\)
  • \(K(\mathbf{x}, \mathbf{y})\): 커널 함수 (두 입력 벡터 \(\mathbf{x}\), \(\mathbf{y}\)에 대한 유사도)
  • \(\phi(\mathbf{x})\): 입력 벡터 \(\mathbf{x}\)를 고차원 특징 공간으로 매핑하는 함수
  • \(\cdot\): 내적(inner product)
• 대표적인 커널 함수:
  • 선형 커널 (Linear Kernel): \(K(\mathbf{x}, \mathbf{y}) = \mathbf{x}^T \mathbf{y}\) (단순 내적)
  • 다항식 커널 (Polynomial Kernel): \(K(\mathbf{x}, \mathbf{y}) = (\gamma \mathbf{x}^T \mathbf{y} + r)^d\)
  • RBF 커널 (Radial Basis Function Kernel, 가우시안 커널): \(K(\mathbf{x}, \mathbf{y}) = \exp(-\gamma \|\mathbf{x} - \mathbf{y}\|^2)\) (가장 널리 사용)
  • 시그모이드 커널 (Sigmoid Kernel): \(K(\mathbf{x}, \mathbf{y}) = \tanh(\gamma \mathbf{x}^T \mathbf{y} + r)\)
• 핵심: SVM에서의 커널은 데이터 간의 유사도를 측정하는 함수이며, 고차원 특징 공간으로의 암묵적인 매핑을 통해 비선형 문제를 해결합니다.

3. 확률론 및 통계에서의 커널 (Kernel Density Estimation)

확률론 및 통계에서 커널은 커널 밀도 추정(Kernel Density Estimation, KDE)에 사용되는, 원점을 중심으로 대칭이고 적분 값이 1인 비음(non-negative) 함수입니다. KDE는 주어진 데이터(샘플)를 바탕으로 확률 밀도 함수(probability density function)를 추정하는 비모수적(non-parametric) 방법입니다.

• 역할: 데이터 포인트 주변의 밀도를 추정하는 데 사용되는 “가중치 함수”입니다.
• 핵심: 각 데이터 포인트에 커널 함수를 “중첩”시켜, 전체 데이터의 분포를 부드럽게(smooth) 표현합니다.
• 수학적 표현: \(\hat{f}(x) = \frac{1}{nh} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right)\)
  • \(\hat{f}(x)\): \(x\)에서의 추정된 확률 밀도
  • \(n\): 데이터 포인트의 개수
  • \(h\): 대역폭(bandwidth) - 커널의 “폭”을 조절하는 파라미터 (smoothing parameter)
  • \(K(\cdot)\): 커널 함수
  • \(x_i\): \(i\)번째 데이터 포인트
• 대표적인 커널 함수:
  • 가우시안 커널 (Gaussian Kernel): \(K(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2}\) (가장 널리 사용)
  • Epanechnikov 커널: \(K(x) = \frac{3}{4}(1 - x^2) \text{ if } |x| \le 1\)
  • Uniform 커널 (Box Kernel): \(K(x) = \frac{1}{2} \text{ if } |x| \le 1\)
• 핵심: KDE에서의 커널은 확률 밀도 함수를 추정하기 위한 가중치 함수 역할을 합니다.

4. 운영체제 커널 (Operating System Kernel)

컴퓨터 과학, 특히 운영체제(Operating System) 분야에서 커널은 운영체제의 핵심 구성 요소입니다. 하드웨어와 응용 프로그램 사이의 인터페이스 역할을 하며, 시스템의 가장 낮은 수준에서 동작합니다.

• 역할:
  • 프로세스 관리
  • 메모리 관리
  • 파일 시스템 관리
  • 입출력(I/O) 관리
  • 하드웨어 자원 관리
• 예시: Linux 커널, Windows NT 커널, macOS의 XNU 커널

요약 및 비교

분야	커널의 의미	핵심 역할
CNN	컨볼루션 연산을 수행하는 필터 (학습 가능한 가중치 행렬)	이미지의 국소적인 특징 추출
SVM	두 데이터 포인트 사이의 유사도를 계산하는 함수 (고차원 특징 공간으로의 암묵적 매핑)	비선형 데이터를 고차원 공간으로 매핑하여 선형 분리 가능하게 만듦
확률론/통계 (KDE)	확률 밀도 함수를 추정하기 위한 가중치 함수	데이터 분포를 부드럽게 추정
운영체제	운영체제의 핵심 구성 요소 (하드웨어와 응용 프로그램 사이의 인터페이스)	시스템 자원 관리, 하드웨어 추상화
선형대수학(Linear Algebra)	선형변환(혹은 행렬)의 영공간(Null space), 즉 \(A\mathbf{x}=\mathbf{0}\)을 만족하는 벡터 \(\mathbf{x}\)의 집합(선형사상 \(T:V→W\)에 대해 $(T)={∈V∣T()=} $)	선형변환의 특성을 나타냄

딥러닝, 특히 CNN에서 “커널”이라고 하면, 대부분의 경우 컨볼루션 필터를 의미합니다. 하지만, SVM이나 가우시안 프로세스와 같은 다른 머신러닝 알고리즘을 접할 때는 커널 함수의 의미로 사용될 수 있음을 기억해야 합니다. 문맥에 따라 “커널”의 의미를 정확하게 파악하는 것이 중요합니다.

7.2 ResNet의 등장

도전과제: 어떻게 하면 신경망의 깊이를 효과적으로 늘리면서도, 기울기 소실/폭주 문제 없이 안정적으로 학습시킬 수 있을까?

연구자의 고뇌: CNN이 이미지 인식에서 뛰어난 성능을 보이면서, 연구자들은 더 깊은 네트워크를 만들고자 했습니다. 그러나 네트워크가 깊어질수록 역전파 과정에서 기울기가 사라지거나(vanishing gradients) 폭발하는(exploding gradients) 문제가 발생하여 학습이 제대로 이루어지지 않았습니다. 단순한 선형 변환의 반복은 깊은 네트워크의 표현력을 제한했습니다. 어떻게 하면 이 근본적인 한계를 극복하고, 신경망의 깊이를 최대한 활용할 수 있을까요?

CNN이 이미지 인식 분야에서 놀라운 성공을 거두자, 연구자들은 자연스럽게 “더 깊은 네트워크가 더 좋은 성능을 낼 수 있지 않을까?”라는 질문을 던졌습니다. 이론적으로는 더 깊은 네트워크가 더 복잡하고 추상적인 특징을 학습할 수 있어야 했습니다. 하지만, 실제로는 네트워크가 깊어질수록 훈련 오차(training error)가 오히려 증가하는 현상이 발생했습니다.

7.2.1 깊은 신경망의 문제와 ResNet의 탄생

2015년, 마이크로소프트 연구팀(Kaiming He et al.)은 이 문제에 대한 획기적인 해결책을 제시하는 논문을 발표했습니다. 이들은 심층 신경망 학습의 어려움이 과적합 때문이 아니라, 훈련 데이터에 대한 오차조차 제대로 줄이지 못하는 최적화(optimization)의 어려움 때문이라는 것을 실험적으로 밝혔습니다.

연구팀은 56층 신경망이 20층 신경망보다 훈련 데이터에서도 더 큰 오차를 보이는 현상을 관찰했습니다. 이는 56층 네트워크가 적어도 20층 네트워크만큼의 성능은 낼 수 있어야 한다는 직관에 어긋나는 결과였습니다. (56층 네트워크가 20층 네트워크의 함수를 표현하는 것은, 나머지 36개 층이 항등 함수, identity mapping을 학습하면 가능) 즉 “왜 신경망은 깊어질수록 단순한 항등 매핑(identity mapping)조차 학습하지 못하는 것일까?”라는 근본적인 질문을 던졌습니다.

이 문제를 해결하기 위해 연구팀이 제안한 것이 바로 잔차 학습 (Residual Learning) 이라는, 매우 단순하면서도 강력한 아이디어입니다. 핵심은 신경망이 직접 목표 함수 \(H(x)\)를 학습하는 대신, 입력 \(x\)와 목표 함수 \(H(x)\)의 차이, 즉 잔차(residual) \(F(x) = H(x) - x\)를 학습하도록 하는 것입니다.

잔차 학습의 수학적 표현:

\(H(x) = F(x) + x\)

• \(x\): 입력
• \(F(x)\): 잔차 함수 (residual function) - 신경망이 학습해야 할 대상
• \(H(x)\): 목표 함수 (desired mapping)

만약 항등 매핑(\(H(x) = x\))이 최적이라면, 신경망은 잔차 함수 \(F(x)\)를 0으로 만드는 것을 학습하면 됩니다. 이는 \(H(x)\) 전체를 학습하는 것보다 훨씬 쉽습니다.

잔차 연결 (Residual Connection / Skip Connection):

잔차 학습의 아이디어를 구현한 것이 바로 잔차 연결(residual connection) 또는 스킵 연결(skip connection)입니다. 잔차 연결은 입력 \(x\)를 레이어의 출력에 직접 더해주는 경로를 만들어 줍니다.

ResNet의 직관적 이해:

ResNet의 잔차 연결은 마치 전자 공학의 피드백(feedback) 회로와 유사합니다. 입력 신호가 레이어를 통과하면서 왜곡되거나 약해지더라도, 원본 신호가 그대로 전달되는 경로(shortcut connection)가 있기 때문에, 정보(그리고 기울기)가 손실 없이 네트워크를 통해 흐를 수 있습니다.

ResNet의 성공:

ResNet은 잔차 학습과 스킵 연결을 통해, 이전에는 훈련이 불가능했던 152층과 같이 매우 깊은 네트워크를 성공적으로 학습시켰습니다. 그 결과, 2015년 ILSVRC (ImageNet Large Scale Visual Recognition Challenge) 대회에서 3.57%라는, 인간의 오류율(약 5%)보다 낮은 놀라운 오류율을 달성하며 우승했습니다.

ResNet의 잔차 연결은 단순하지만 매우 강력한 아이디어로, 이후 딥러닝 아키텍처 발전에 지대한 영향을 미쳤습니다.

• Transformer (2017): 자연어 처리 분야의 혁명을 가져온 Transformer 아키텍처는 ResNet의 스킵 연결을 “Add & Norm” 레이어의 형태로 채택했습니다.
• DenseNet (2017): DenseNet은 ResNet의 아이디어를 확장하여, 모든 층이 이전 층들의 출력과 직접 연결되는 “dense connection”을 사용했습니다.
• Inception-ResNet: GoogLeNet의 Inception 모듈과 ResNet의 잔차 연결을 결합한 모델입니다.
• EfficientNet, MobileNetV2: EfficientNet, MobileNetV2 등 경량 네트워크들도 ResNet의 잔차 학습 개념을 채택했습니다.

7.2.2 ResNet의 구조와 핵심 요소

ResNet은 크게 두 가지 유형의 블록, 즉 기본 블록(Basic Block)과 병목 블록(Bottleneck Block)을 사용하여 구성됩니다.

• 기본 블록 (Basic Block): ResNet-18과 ResNet-34에서 사용됩니다. 두 개의 3x3 컨볼루션 층으로 구성되며, 각 컨볼루션 층 뒤에는 배치 정규화(Batch Normalization)와 ReLU 활성화 함수가 뒤따릅니다. 그리고 가장 중요한 잔차 연결(residual connection)이 이 두 층의 입력을 출력에 더해주는 형태로 구성됩니다.

import torch
import torch.nn as nn
import torch.nn.functional as F

class BasicBlock(nn.Module):
    """Basic block for ResNet
    Consists of two 3x3 convolutional layers
    """
    expansion = 1  # Output channel expansion factor

    def __init__(self, in_channels, out_channels, stride=1):
        super().__init__()
        # First convolutional layer
        self.conv1 = nn.Conv2d(in_channels, out_channels,
                              kernel_size=3, stride=stride, padding=1)
        self.bn1 = nn.BatchNorm2d(out_channels)

        # Second convolutional layer
        self.conv2 = nn.Conv2d(out_channels, out_channels * self.expansion,
                              kernel_size=3, stride=1, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channels * self.expansion)

        # Skip connection (adjust dimensions with 1x1 convolution if necessary)
        self.shortcut = nn.Sequential()
        if stride != 1 or in_channels != out_channels * self.expansion:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels * self.expansion,
                         kernel_size=1, stride=stride),
                nn.BatchNorm2d(out_channels * self.expansion)
            )

    def forward(self, x):
        # Main path
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))

        # Add skip connection
        out += self.shortcut(x)
        out = F.relu(out)
        return out

• 잔차 연결 (Residual Connection): out += self.shortcut(x) 부분이 핵심입니다. 입력을 바로 출력에 더해줍니다.
• 차원 조정: 만약 입력 채널 수와 출력 채널 수가 다르거나, stride가 1이 아니라서 특징 맵의 크기가 달라지는 경우에는, self.shortcut을 통해 1x1 컨볼루션을 적용하여 채널 수와 크기를 맞춰줍니다.

병목 블록 (Bottleneck Block)

ResNet-50 이상에서 사용됩니다. 더 깊은 네트워크를 효율적으로 만들기 위해 사용됩니다. 1x1, 3x3, 1x1 컨볼루션의 조합으로 구성되어, 마치 병목(bottleneck)처럼 채널 수를 줄였다가 다시 늘리는 구조를 가집니다.

class Bottleneck(nn.Module):
    """병목(Bottleneck) 구조 구현"""
    
    expansion = 4  # 출력 채널을 4배로 확장하는 상수

    def __init__(self, in_channels, out_channels, stride=1):
        """
        Args:
            in_channels: 입력 채널 수
            out_channels: 중간 처리 채널 수 (최종 출력은 이것의 expansion배)
            stride: 스트라이드 크기 (기본값: 1)
        """
        super().__init__()

        # 1단계: 1x1 컨볼루션으로 채널 수를 줄임 (차원 감소)
        # 예: 256 -> 64 채널로 감소
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=1)
        self.bn1 = nn.BatchNorm2d(out_channels)
        
        # 2단계: 3x3 컨볼루션으로 특징 추출 (병목 구간)
        # 감소된 채널 수로 연산 수행 (예: 64채널에서 처리)
        self.conv2 = nn.Conv2d(out_channels, out_channels, 
                              kernel_size=3, stride=stride, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channels)
        
        # 3단계: 1x1 컨볼루션으로 채널 수를 다시 늘림 (차원 복원)
        # 예: 64 -> 256 채널로 확장 (expansion=4인 경우)
        self.conv3 = nn.Conv2d(out_channels, 
                              out_channels * self.expansion, kernel_size=1)
        self.bn3 = nn.BatchNorm2d(out_channels * self.expansion)

병목(Bottleneck) 구조는 그 이름이 암시하듯 병의 목처럼 채널의 차원이 좁아졌다가 다시 넓어지는 형태를 가집니다. 예를 들어 256개의 입력 채널을 가진 특징 맵이라고 가정하면

1. 첫 번째 1x1 컨볼루션으로 256→64로 차원을 줄임

2. 3x3 컨볼루션을 줄어든 64 채널에서 수행

3. 마지막 1x1 컨볼루션으로 64→256으로 차원을 복원

이러한 구조는 다음과 같은 장점이 있습니다. - 계산량 감소: 가장 비용이 큰 3x3 컨볼루션을 적은 채널에서 수행 - 파라미터 수 감소: 전체 파라미터 수가 기본 블록 대비 크게 감소 - 표현력 유지: 차원을 늘리는 과정에서 다양한 특징 학습 능력 보존

이러한 효율성 덕분에 ResNet-50 이상의 깊은 모델에서는 기본 블록 대신 병목 구조를 채택하고 있습니다.

스킵 연결에는 두 가지 형태가 있습니다. 입출력 채널 수가 같으면 직접 연결하고, 다르면 1x1 컨볼루션으로 채널 수를 맞춥니다. 이는 GoogLeNet(2014년)의 인셉션 모듈에서 영감을 받았습니다.

ResNet은 이러한 기본 블록 또는 병목 블록을 여러 개 쌓아서 깊은 네트워크를 구성합니다.

ResNet은 네트워크의 깊이에 따라 다양한 버전(ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152 등)이 있습니다.

• ResNet-18, ResNet-34: 기본 블록(Basic Block)을 사용합니다.
• ResNet-50, ResNet-101, ResNet-152: 병목 블록(Bottleneck Block)을 사용합니다.

ResNet의 일반적인 구조는 다음과 같습니다.

1. 초기 컨볼루션 층: 7x7 컨볼루션과 최대 풀링(max pooling)을 사용하여 입력 이미지의 크기를 줄입니다.
2. 여러 개의 스테이지 (Stage): 각 스테이지는 여러 개의 블록(기본 블록 또는 병목 블록)으로 구성됩니다. 각 스테이지의 첫 번째 블록에서는 stride를 2로 설정하여 특징 맵의 크기를 절반으로 줄입니다(다운샘플링).
3. 평균 풀링 (Average Pooling): 특징 맵의 공간적 차원을 제거합니다. (global average pooling)
4. 완전 연결 층 (Fully Connected Layer): 클래스 분류를 수행합니다.

네트워크 깊이와 블록 수:

ResNet의 깊이는 각 스테이지별 블록 수에 의해 결정됩니다. 예를 들어, ResNet-18은 각 스테이지에 2개의 기본 블록을 사용합니다 ([2, 2, 2, 2]). ResNet-50은 각 스테이지에 [3, 4, 6, 3]개의 병목 블록을 사용합니다.

• ResNet-18:
  • 초기 7x7 컨볼루션: 1층
  • 기본 블록 (2개의 3x3 컨볼루션): 2층 x (2 + 2 + 2 + 2) = 16층
  • 최종 완전 연결 층: 1층
  • 총 1 + 16 + 1 = 18층

# 총 층수 = 1 + (2 × 2 + 2 × 2 + 2 × 2 + 2 × 2) + 1 = 18
def ResNet18(num_classes=10):
    return ResNet(BasicBlock, [2, 2, 2, 2], num_classes) # 기본 블록 사용

• ResNet-50:
  • 초기 7x7 컨볼루션: 1층
  • 병목 블록 (3개의 컨볼루션): 3층 x (3 + 4 + 6 + 3) = 48층
  • 최종 완전 연결 층: 1층
  • 총 1 + 48 + 1 = 50층

# 병목 블록: 1x1 → 3x3 → 1x1 구조
# 총 층수 = 1 + (3 × 3 + 3 × 4 + 3 × 6 + 3 × 3) + 1 = 50
def ResNet50(num_classes=10):
    return ResNet(Bottleneck, [3, 4, 6, 3], num_classes) # 병목 블록 사용

ResNet 설계 원칙:

• 4개의 스테이지: 각 스테이지마다 특징 맵의 크기는 절반으로 줄이고, 채널 수는 2배로 늘립니다. 이는 VGGNet의 설계 철학을 따른 것입니다.
• 중간 스테이지에 더 많은 블록 배치: 일반적으로 중간 스테이지(stage 3)에 더 많은 블록을 배치합니다. 이는 중간 수준의 특징이 객체 인식에서 중요하다는 경험적 증거에 기반합니다.
• 병목 구조 (깊은 네트워크): 네트워크가 깊어질수록 계산 효율성을 위해 병목 구조를 사용합니다.

이러한 구조적 혁신 덕분에 ResNet은 매우 깊은 네트워크를 효율적으로 학습할 수 있었고, 이는 현대 딥러닝 아키텍처의 표준이 되었습니다. ResNet의 아이디어는 이후 Wide ResNet, ResNeXt, DenseNet 등 다양한 변형 모델에 영향을 미쳤습니다.

7.2.4 ResNet의 훈련과 특징 추출 시각화

ResNet-18 모델을 FashionMNIST 데이터셋으로 훈련시키는 예제는 chapter_07/train_resnet.py에 있습니다.

from dldna.chapter_07.train_resnet import train_resnet18, save_model

model = train_resnet18(epochs=10)
# Save the model
save_model(model)

ResNet이 어떻게 이미지의 특징을 추출하는지 실제로 확인해보겠습니다. 훈련된 ResNet-18 모델을 사용하여 각 층을 통과할 때마다 특징 맵이 어떻게 변화하는지 시각화하겠습니다.

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from dldna.chapter_07.resnet import ResNet18
from dldna.chapter_07.train_resnet import get_trained_model_and_test_image
from torchvision import datasets, transforms

%matplotlib inline

def visualize_features(model, image):
    """각 층의 특징 맵을 시각화하는 함수"""
    features = {}
    
    # 특징 맵을 저장할 훅 등록
    def get_features(name):
        def hook(model, input, output):
            features[name] = output.detach()
        return hook

    # 각 주요 층에 훅 등록
    model.conv1.register_forward_hook(get_features('conv1'))
    for idx, layer in enumerate(model.layer1):
        layer.register_forward_hook(get_features(f'layer1_{idx}'))
    for idx, layer in enumerate(model.layer2):
        layer.register_forward_hook(get_features(f'layer2_{idx}'))
    for idx, layer in enumerate(model.layer3):
        layer.register_forward_hook(get_features(f'layer3_{idx}'))
    for idx, layer in enumerate(model.layer4):
        layer.register_forward_hook(get_features(f'layer4_{idx}'))

    # 모델에 이미지 통과
    with torch.no_grad():
        _ = model(image.unsqueeze(0))

    # 특징 맵 시각화
    plt.figure(figsize=(20, 10))
    for idx, (name, feature) in enumerate(features.items(), 1):
        plt.subplot(3, 6, idx)
        # 각 층의 첫 번째 채널만 시각화
        plt.imshow(feature[0, 0].cpu(), cmap='viridis')
        plt.title(f'Layer: {name}')
        plt.axis('off')
    
    plt.tight_layout()
    plt.show()
    
    return features

model, test_image, label, pred, classes = get_trained_model_and_test_image()

# 원본 이미지 시각화
plt.figure(figsize=(4, 4))
plt.imshow(test_image.squeeze(), cmap='gray')
plt.title(f'Class: {classes[label]}')
plt.axis('off')
plt.show()

print(f"이미지 shape: {test_image.shape}")
print(f"실제 클래스: {classes[label]} (레이블: {label})")
print(f"예측 클래스: {classes[pred]} (레이블: {pred})")

# # ResNet 모델에 이미지 통과시키고 특징 맵 시각화
# model = ResNet18(in_channels=1, num_classes=10)
# model.load_state_dict(torch.load('../../models/resnet18_fashion.pth'))
# model.eval()

features = visualize_features(model, test_image)

이미지 shape: torch.Size([1, 224, 224])
실제 클래스: Ankle boot (레이블: 9)
예측 클래스: Ankle boot (레이블: 9)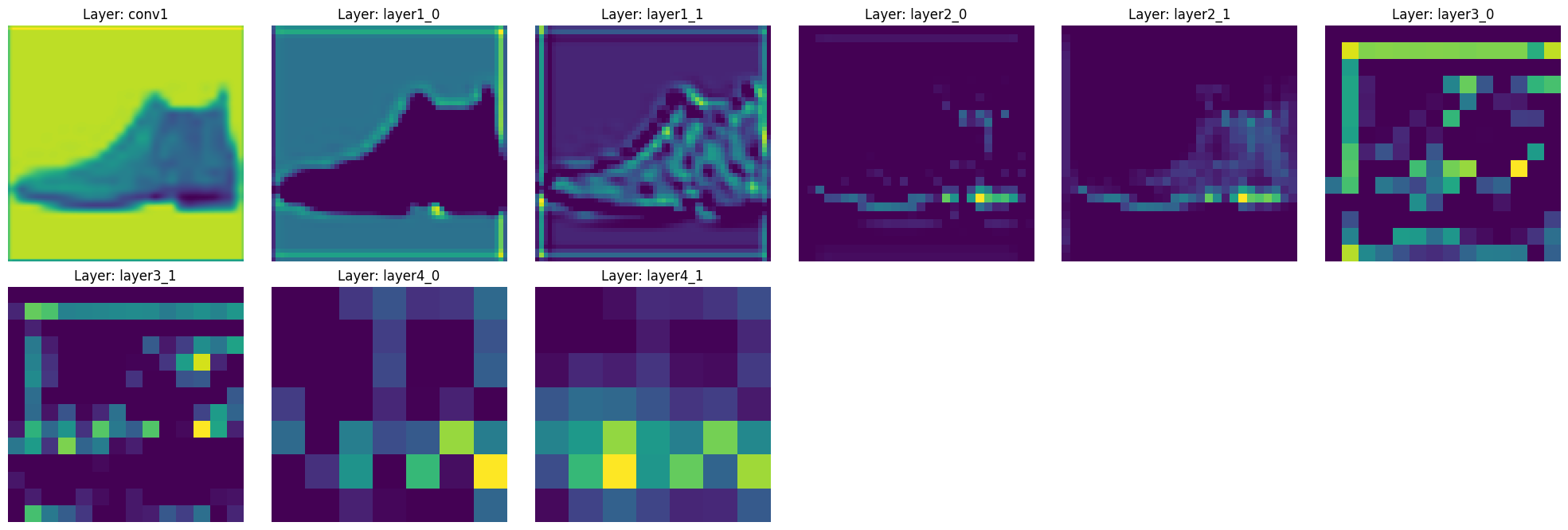

이 코드를 실행하면 ResNet-18의 주요 층들을 통과하면서 특징이 어떻게 변화하는지 볼 수 있습니다.

1. 초기 컨볼루션 (conv1) : 기본적인 형태 정보 추출, 에지와 텍스처 같은 저수준 특징 검출
2. layer1 (초기 잔차 블록) : 지역적 특징들의 결합하고 단순한 패턴 조합 시작
3. layer2 : 특징 맵의 크기는 줄어들지만 채널 수 증가하면서 더 복잡한 패턴 인식
4. layer3 : 추상화 수준이 더 높아지면서 객체의 부분적 특징 검출
5. layer4 (최종 잔차 블록) : 클래스 구분 가능하게 필요한 추상적 고수준 특징을 추출

이러한 계층적 특징 추출은 ResNet의 핵심 강점 중 하나입니다. 스킵 연결 덕분에 각 층의 특징이 잘 보존되면서도 점진적으로 추상화되는 것을 확인할 수 있습니다.

클릭하여 내용 보기 (딥다이브: Inception 모듈 - CNN에 다양성과 효율성을 더하다)

Inception 모듈 - CNN에 다양성과 효율성을 더하다

Inception 모듈은 2014년 ImageNet Large Scale Visual Recognition Challenge (ILSVRC)에서 우승한 GoogLeNet[^1]의 핵심 구성 요소입니다. 이 모듈은 “Network in Network”라는 별명처럼, 기존의 CNN 구조에 대한 새로운 접근 방식을 제시했습니다. ResNet이 “깊이(depth)”의 문제를 해결했다면, Inception 모듈은 “다양성(diversity)”과 “효율성(efficiency)”이라는 두 가지 중요한 문제를 동시에 해결했습니다. 이 딥다이브에서는 Inception 모듈의 핵심 아이디어, 수학적 원리, 그리고 진화 과정을 심층적으로 분석하고, 딥러닝, 특히 CNN 아키텍처 설계에 어떤 영향을 미쳤는지 살펴봅니다.

Inception 모듈의 핵심 아이디어: “Multi-Scale” 특징 추출

Inception 모듈은 이 문제에 대한 우아한 해결책을 제시합니다. 바로 다양한 크기의 필터를 병렬적으로 사용하고, 그 결과(feature map)를 결합(concatenate)하는 것입니다.

핵심 아이디어:

1. 다양한 필터: 1x1, 3x3, 5x5 등 다양한 크기의 컨볼루션 필터를 동일한 입력에 대해 적용합니다.
2. 병렬 처리: 각 필터는 독립적으로 컨볼루션 연산을 수행합니다.
3. 결합 (Concatenation): 각 필터에서 생성된 특징 맵(feature map)을 채널(channel) 축을 따라 결합합니다.
4. 1x1 컨볼루션: 계산 비용을 줄이고, 비선형성을 추가하며, 채널 간 정보를 혼합합니다. (“병목 층” 역할)

Inception Module v1 (GoogLeNet, 2014)

Inception 모듈의 첫 번째 버전(GoogLeNet, [^1])은 다음과 같은 구조를 가집니다.

• 입력: 이전 층의 특징 맵(feature map)
• 병렬 가지(Branches):
  • 1x1 컨볼루션
  • 1x1 컨볼루션 -> 3x3 컨볼루션
  • 1x1 컨볼루션 -> 5x5 컨볼루션
  • 3x3 최대 풀링(max pooling) -> 1x1 컨볼루션
• 출력: 각 가지의 출력을 채널 축으로 결합(concatenate)

1x1 컨볼루션의 역할:

1x1 컨볼루션은 Inception 모듈에서 매우 중요한 역할을 합니다.

• 차원 축소 (Dimensionality Reduction): 1x1 컨볼루션은 채널 수를 줄이는 데 사용됩니다. 3x3이나 5x5 컨볼루션 전에 1x1 컨볼루션을 사용하여 채널 수를 줄이면, 계산량을 크게 줄일 수 있습니다. (병목층, Bottleneck Layer)
• 비선형성 추가: 1x1 컨볼루션 뒤에 ReLU와 같은 활성화 함수를 추가하여 네트워크에 비선형성을 더할 수 있습니다.
• 채널 간 정보 혼합: 1x1 컨볼루션은 입력 채널들의 선형 조합을 계산하므로, 채널 간의 정보를 혼합하는 효과를 냅니다.

Inception Module v1의 한계:

• 5x5 컨볼루션은 여전히 계산 비용이 큽니다.
• 풀링 연산은 차원 축소는 하지만, 정보 손실을 유발할 수 있습니다.

Inception Module v2 & v3 (2015)

Inception v2와 v3는 v1의 한계를 개선하기 위해 다음과 같은 아이디어를 도입했습니다 [^2].

• Factorization: 5x5 컨볼루션을 3x3 컨볼루션 2개로 분해합니다. (계산량 감소)
• Asymmetric Convolution: 3x3 컨볼루션을 1x3 컨볼루션과 3x1 컨볼루션으로 분해합니다.
• Auxiliary Classifier: 훈련 중간에 보조 분류기(auxiliary classifier)를 추가하여 기울기 소실 문제를 완화하고, 학습을 가속화합니다. (v3에서 제거)
• Label Smoothing: 정답 레이블에 약간의 노이즈를 추가하여 모델이 과도하게 확신하는 것을 방지합니다 (overconfidence).

Inception Module v4 (2016)

Inception-v4는 Inception-ResNet 모듈을 도입하여, Inception 모듈과 ResNet의 잔차 연결(residual connection)을 결합했습니다 [^3].

Xception (2017)

Xception (“Extreme Inception”)은 Inception 모듈의 아이디어를 극한으로 확장한 모델입니다[^4]. Depthwise Separable Convolution을 사용하여, 채널별 공간 방향 컨볼루션(depthwise convolution)과 채널 간 컨볼루션(pointwise convolution, 1x1 conv)을 분리합니다.

수학적 표현 (Inception v1)

Inception 모듈의 각 가지(branch)는 다음과 같이 표현할 수 있습니다.

• Branch 1: \(\text{Output}_1 = \text{Conv}_{1x1}(\text{Input})\)
• Branch 2: \(\text{Output}_2 = \text{Conv}_{3x3}(\text{Conv}_{1x1}(\text{Input}))\)
• Branch 3: \(\text{Output}_3 = \text{Conv}_{5x5}(\text{Conv}_{1x1}(\text{Input}))\)
• Branch 4: \(\text{Output}_4 = \text{Conv}_{1x1}(\text{MaxPool}(\text{Input}))\)
• Output: \(\text{Concatenate}(\text{Output}_1, \text{Output}_2, \text{Output}_3, \text{Output}_4)\)

여기서 \(\text{Conv}_{NxN}\)은 \(N \times N\) 크기의 컨볼루션 연산을, \(\text{MaxPool}\)은 최대 풀링 연산을 나타냅니다.

웨이블릿 변환과의 유사성

Inception 모듈의 다중 스케일(multi-scale) 접근 방식은 웨이블릿 변환(wavelet transform)과 유사한 점이 있습니다. 웨이블릿 변환은 신호를 다양한 주파수 성분으로 분해하는 방법입니다. Inception 모듈의 각 필터(1x1, 3x3, 5x5)는 서로 다른 주파수 대역, 즉, 서로 다른 스케일의 특징을 추출하는 것으로 해석할 수 있습니다. 1x1 컨볼루션은 고주파 성분, 3x3은 중간, 5x5는 저주파 성분을 추출한다고 볼 수 있습니다.

Inception 모듈의 장점

• 다양한 스케일의 특징 추출: 여러 크기의 필터를 동시에 사용함으로써, 이미지 내의 다양한 크기의 특징을 효과적으로 포착합니다.
• 계산 효율성: 1x1 컨볼루션을 사용하여 차원을 줄임으로써, 계산량을 줄이면서도 표현력을 유지합니다.
• 강력한 성능: ImageNet 데이터셋에서 최고 수준의 성능을 달성했습니다.

딥러닝 생태계에 미친 영향

Inception 모듈은 CNN 아키텍처 설계에 대한 새로운 관점을 제시했습니다. “더 깊게(deeper)” 가는 것뿐만 아니라, “더 넓게(wider)” 그리고 “더 다양하게(more diverse)” 가는 것이 중요하다는 것을 보여주었습니다. Inception 모듈의 아이디어는 이후 MobileNet, ShuffleNet 등 경량 모델 개발에도 영향을 미쳤습니다.

간단한 Inception 모듈 구현 (PyTorch)

import torch
import torch.nn as nn
import torch.nn.functional as F

class InceptionModule(nn.Module):
    def __init__(self, in_channels, out_channels_1x1, out_channels_3x3_reduce,
                 out_channels_3x3, out_channels_5x5_reduce, out_channels_5x5,
                 out_channels_pool):
        super().__init__()

        # 1x1 conv branch
        self.branch1x1 = nn.Conv2d(in_channels, out_channels_1x1, kernel_size=1)

        # 1x1 conv -> 3x3 conv branch
        self.branch3x3_reduce = nn.Conv2d(in_channels, out_channels_3x3_reduce, kernel_size=1)
        self.branch3x3 = nn.Conv2d(out_channels_3x3_reduce, out_channels_3x3, kernel_size=3, padding=1)

        # 1x1 conv -> 5x5 conv branch
        self.branch5x5_reduce = nn.Conv2d(in_channels, out_channels_5x5_reduce, kernel_size=1)
        self.branch5x5 = nn.Conv2d(out_channels_5x5_reduce, out_channels_5x5, kernel_size=5, padding=2)

        # 3x3 max pool -> 1x1 conv branch
        self.branch_pool = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.branch_pool_proj = nn.Conv2d(in_channels, out_channels_pool, kernel_size=1)

    def forward(self, x):
        branch1x1 = F.relu(self.branch1x1(x))

        branch3x3 = F.relu(self.branch3x3_reduce(x))
        branch3x3 = F.relu(self.branch3x3(branch3x3))

        branch5x5 = F.relu(self.branch5x5_reduce(x))
        branch5x5 = F.relu(self.branch5x5(branch5x5))

        branch_pool = F.relu(self.branch_pool_proj(self.branch_pool(x)))

        outputs = [branch1x1, branch3x3, branch5x5, branch_pool]
        return torch.cat(outputs, 1)  # Concatenate along the channel dimension

# Example Usage
in_channels = 3  # Example input channels
out_channels_1x1 = 64
out_channels_3x3_reduce = 96
out_channels_3x3 = 128
out_channels_5x5_reduce = 16
out_channels_5x5 = 32
out_channels_pool = 32

inception_module = InceptionModule(in_channels, out_channels_1x1, out_channels_3x3_reduce,
                                  out_channels_3x3, out_channels_5x5_reduce, out_channels_5x5,
                                  out_channels_pool)

# Example input tensor (batch_size, channels, height, width)
input_tensor = torch.randn(1, in_channels, 28, 28)
output_tensor = inception_module(input_tensor)
print(output_tensor.shape)  # Check output shape

이 코드는 Inception Module (v1)의 기본 구조를 PyTorch로 구현한 것입니다. torchvision.models 나 timm 라이브러리에는 더 발전된 버전의 Inception 네트워크(Inception-v3, Inception-v4, Inception-ResNet 등)가 구현되어 있으므로, 실제 프로젝트에서는 이러한 라이브러리를 사용하는 것이 좋습니다.

---

[1]: Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., … & Rabinovich, A. (2015). Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1-9).

[2]: Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., & Wojna, Z. (2016). Rethinking the inception architecture for computer vision. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 2818-2826).

[3]: Szegedy, C., Ioffe, S., Vanhoucke, V., & Alemi, A. A. (2017). Inception-v4, inception-resnet and the impact of residual connections on learning. In Thirty-first AAAI conference on artificial intelligence.

[4]: Chollet, F. (2017). Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1251-1258).

7.3 EfficientNet: 효율적인 모델 스케일링

도전과제: 어떻게 하면 모델의 성능을 극대화하면서도, 계산 비용(파라미터 수, FLOPS)을 최소화할 수 있을까?

연구자의 고뇌: ResNet의 등장으로 깊은 네트워크를 학습시키는 것이 가능해졌지만, 모델의 크기를 어떻게 조절해야 할지에 대한 체계적인 방법은 없었습니다. 단순히 층을 더 쌓거나, 채널 수를 늘리는 것은 계산 비용을 크게 증가시킬 수 있습니다. 연구자들은 모델의 깊이(depth), 너비(width), 해상도(resolution) 사이의 최적의 균형을 찾고, 이를 통해 주어진 계산 자원 하에서 최고의 성능을 달성하는 방법을 찾고자 했습니다.

7.3.1 Compound Scaling: 깊이, 너비, 해상도의 균형

EfficientNet의 핵심 아이디어는 “Compound Scaling”입니다. 이전의 연구들이 모델의 깊이, 너비, 해상도 중 하나만 조절하는 경향이 있었다면, EfficientNet은 이 세 가지 요소를 동시에, 균형 있게 조절하는 것이 더 효율적이라는 것을 발견했습니다.

• 깊이 (Depth): 네트워크의 층 수입니다. 더 깊은 네트워크는 더 복잡한 특징을 학습할 수 있지만, 기울기 소실/폭주 문제와 과적합 문제가 발생하기 쉽습니다.
• 너비 (Width): 각 층의 채널 수 (필터 수)입니다. 더 넓은 네트워크는 더 미세한 특징(fine-grained features)을 학습할 수 있지만, 계산 비용과 파라미터 수가 증가하고 과적합의 위험이 있습니다.
• 해상도 (Resolution): 입력 이미지의 크기입니다. 더 높은 해상도의 이미지는 더 많은 정보를 담고 있지만, 계산 비용이 크게 증가합니다.

EfficientNet은 이 세 가지 요소가 서로 연관되어 있으며, 하나의 요소만 변경하는 것보다 균형 있게 함께 조절하는 것이 더 효과적이라는 것을 실험적으로 보였습니다. 예를 들어, 이미지 해상도를 2배 높이면, 네트워크가 더 미세한 패턴을 학습할 수 있도록 깊이와 너비를 적절히 증가시켜야 합니다. 단순히 해상도만 높이면 성능 향상이 미미하거나 오히려 떨어질 수 있습니다.

EfficientNet 논문에서는 모델 스케일링 문제를 최적화 문제로 정의하고, 깊이(depth), 너비(width), 해상도(resolution) 사이의 관계를 다음과 같은 수식으로 표현했습니다.

먼저, CNN 모델을 \(\mathcal{N}\)이라고 할 때, \(i\)번째 레이어는 함수 변환 \(Y_i = \mathcal{F}_i(X_i)\) 로 나타낼 수 있습니다. 여기서 \(Y_i\)는 출력 텐서, \(X_i\)는 입력 텐서, \(\mathcal{F}_i\)는 연산(operator)입니다. 입력 텐서 \(X_i\)의 형태는 \(<H_i, W_i, C_i>\) 와 같이 표현할 수 있는데, 각각 높이(height), 너비(width), 채널(channel) 수를 의미합니다.

전체 CNN 모델 \(\mathcal{N}\)은 각 레이어의 합성 함수(composition)로 나타낼 수 있습니다

\(\mathcal{N} = \mathcal{F}_k \circ \mathcal{F}_{k-1} \circ ... \circ \mathcal{F}_1 = \bigodot_{i=1...k} \mathcal{F}_i\)

일반적인 CNN 설계에서는 최적의 레이어 연산 \(\mathcal{F}_i\)를 찾는 데 집중하지만, EfficientNet은 레이어 연산은 고정한 채, 네트워크의 길이(\(\hat{L}_i\)), 너비(\(\hat{C}_i\)), 해상도(\(\hat{H}_i, \hat{W}_i\))를 조절하는 데 초점을 맞춥니다. 이를 위해 기준 네트워크(baseline network)를 \(\hat{\mathcal{N}}\)으로 정의하고, 여기에 스케일링 계수를 곱하여 모델을 확장합니다.

기준 네트워크: \(\hat{\mathcal{N}} = \bigodot_{i=1...s} \hat{\mathcal{F}}_i^{L_i}(X_{<H_i, W_i, C_i>})\)

EfficientNet은 다음의 최적화 문제를 해결하고자 합니다.

\(\underset{\mathcal{N}}{maximize}\quad Accuracy(\mathcal{N})\)

\(subject\ to\quad \mathcal{N} = \bigodot_{i=1...s} \hat{\mathcal{F}}_i^{d \cdot \hat{L}_i}(X_{<r \cdot \hat{H}_i, r \cdot \hat{W}_i, w \cdot \hat{C}_i>})\)

\(Memory(\mathcal{N}) \leq target\_memory\)

\(FLOPS(\mathcal{N}) \leq target\_flops\)

여기서 \(d\), \(w\), \(r\)은 각각 깊이, 너비, 해상도의 스케일링 계수입니다.

EfficientNet은 이 문제를 해결하기 위해, 모든 자원 제약 조건(resource constraints)을 동시에 만족하면서 정확도를 최대화하는 복잡한 최적화 문제를 단순화하는 Compound Scaling 방법을 제안합니다. Compound scaling은 하나의 계수(\(\phi\), compound coefficient)를 사용하여 깊이, 너비, 해상도를 균일하게 조절합니다.

\(\begin{aligned} & \text{depth: } d = \alpha^{\phi} \\ & \text{width: } w = \beta^{\phi} \\ & \text{resolution: } r = \gamma^{\phi} \\ & \text{subject to } \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \\ & \alpha \geq 1, \beta \geq 1, \gamma \geq 1 \end{aligned}\)

• \(\phi\) (phi)는 사용자가 지정하는 계수(compound coefficient)로, 전체적인 모델 크기를 조절합니다.
• \(\alpha\), \(\beta\), \(\gamma\)는 각각 깊이, 너비, 해상도를 얼마나 늘릴지를 결정하는 상수입니다. 이 값들은 작은 그리드 탐색(small grid search)을 통해 결정됩니다. (\(\alpha\), \(\beta\), \(\gamma\) 값을 찾기 위해, \(\phi=1\) 로 고정하고 작은 탐색을 수행합니다.)
• 제약 조건 (\(α ⋅ β² ⋅ γ² ≈ 2\))은 \(ϕ\)를 1 증가시킬 때마다 모델의 FLOPS가 대략 2배 증가하도록 합니다. 이 제약 조건은 FLOPS가 깊이에 대해서는 선형적으로, 너비와 해상도에 대해서는 제곱으로 증가하기 때문에 설정되었습니다.

이 compound scaling 방법을 사용하면, 사용자는 \(ϕ\) 값 하나만 조정하여 모델의 크기를 쉽게 조절할 수 있으며, 모델의 성능과 효율성 사이의 균형을 효과적으로 제어할 수 있습니다.

7.3.2 EfficientNet 아키텍처

EfficientNet은 AutoML (Neural Architecture Search, NAS) 기술을 사용하여 최적의 기본 모델(baseline model)인 EfficientNet-B0를 찾고, 여기에 compound scaling을 적용하여 다양한 크기의 모델(B1 ~ B7, 그리고 더 큰 L2까지)을 생성했습니다.

EfficientNet-B0의 구조:

EfficientNet-B0는 MobileNetV2에서 영감을 받은 MBConv (Mobile Inverted Bottleneck Convolution) 블록을 기반으로 합니다. MBConv 블록은 계산 효율성을 높이기 위해 다음과 같은 구조를 가집니다.

1. Expansion (1x1 Conv): 입력 채널 수를 확장합니다 (expansion factor, 보통 6). 1x1 컨볼루션을 사용하여 채널 수를 늘리면, subsequent 연산(depthwise convolution)의 계산 비용을 상대적으로 줄이면서도 표현력을 높일 수 있습니다.

2. Depthwise Separable Convolution:

   • Depthwise Convolution (3x3): 각 입력 채널에 대해 독립적으로 공간 방향 컨볼루션을 수행합니다. 일반적인 컨볼루션과 달리, 채널 간의 정보 혼합은 일어나지 않습니다.
   • Pointwise Convolution (1x1 Conv): 1x1 컨볼루션을 사용하여 채널 간의 정보를 혼합합니다.

   Depthwise separable convolution은 일반적인 컨볼루션보다 파라미터 수와 계산량을 크게 줄일 수 있습니다.

3. Squeeze-and-Excitation (SE) Block: 채널 간의 중요도를 학습하여, 중요한 채널을 강조합니다. SE 블록은 전역 평균 풀링(global average pooling)을 사용하여 각 채널의 정보를 요약하고, 두 개의 fully connected layer를 사용하여 채널별 가중치를 계산합니다.

4. Projection (1x1 Conv): 채널 수를 다시 원래대로 줄입니다. (residual connection을 위해)

5. Residual Connection: 입력과 출력을 더합니다. (입력 채널 수와 출력 채널 수가 같을 때, stride=1일 때). ResNet의 핵심 아이디어입니다.

다음은 PyTorch를 사용하여 EfficientNet-B0의 MBConv 블록을 구현한 예제입니다. (전체 EfficientNet-B0 구현은 생략합니다. torchvision 또는 timm 라이브러리에서 불러올 수 있습니다.)

import torch
import torch.nn as nn
import torch.nn.functional as F

class MBConvBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride, expand_ratio=6, se_ratio=0.25, kernel_size=3):
        super().__init__()

        self.stride = stride
        self.use_residual = (in_channels == out_channels) and (stride == 1) # 잔차 연결 조건

        expanded_channels = in_channels * expand_ratio

        # Expansion (1x1 conv)
        self.expand_conv = nn.Conv2d(in_channels, expanded_channels, kernel_size=1, bias=False)
        self.bn0 = nn.BatchNorm2d(expanded_channels)

        # Depthwise convolution
        self.depthwise_conv = nn.Conv2d(expanded_channels, expanded_channels, kernel_size=kernel_size,
                                       stride=stride, padding=kernel_size//2, groups=expanded_channels, bias=False)
                                       # groups=expanded_channels: depthwise conv
        self.bn1 = nn.BatchNorm2d(expanded_channels)

        # Squeeze-and-Excitation
        num_reduced_channels = max(1, int(in_channels * se_ratio))  # 최소 1개는 유지
        self.se_reduce = nn.Conv2d(expanded_channels, num_reduced_channels, kernel_size=1)
        self.se_expand = nn.Conv2d(num_reduced_channels, expanded_channels, kernel_size=1)

        # Pointwise convolution (projection)
        self.project_conv = nn.Conv2d(expanded_channels, out_channels, kernel_size=1, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channels)

    def forward(self, x):
        identity = x

        # Expansion
        out = F.relu6(self.bn0(self.expand_conv(x)))

        # Depthwise separable convolution
        out = F.relu6(self.bn1(self.depthwise_conv(out)))

        # Squeeze-and-Excitation
        se = out.mean((2, 3), keepdim=True)  # Global Average Pooling
        se = F.relu6(self.se_reduce(se))
        se = torch.sigmoid(self.se_expand(se))
        out = out * se  # 채널별 가중치 곱

        # Projection
        out = self.bn2(self.project_conv(out))

        # Residual connection
        if self.use_residual:
            out = out + identity

        return out

# Example usage
# in_channels = 32
# out_channels = 16
# stride = 1
# mbconv_block = MBConvBlock(in_channels, out_channels, stride)
# input_tensor = torch.randn(1, in_channels, 224, 224)  # Example input
# output_tensor = mbconv_block(input_tensor)
# print(output_tensor.shape)

7.3.3 EfficientNet의 성능 및 영향

EfficientNet은 ImageNet 분류에서 기존의 CNN 모델들(ResNet, DenseNet, Inception 등)보다 훨씬 적은 파라미터와 계산량으로 더 높은 정확도를 달성했습니다. 아래 표는 EfficientNet과 다른 모델들의 성능을 비교한 것입니다.

Model	Top-1 Accuracy	Top-5 Accuracy	Parameters	FLOPS
ResNet-50	76.0%	93.0%	25.6M	4.1B
DenseNet-169	76.2%	93.2%	14.3M	3.4B
Inception-v3	77.9%	93.8%	23.9M	5.7B
EfficientNet-B0	77.1%	93.3%	5.3M	0.39B
EfficientNet-B1	79.1%	94.4%	7.8M	0.70B
EfficientNet-B4	82.9%	96.4%	19.3M	4.2B
EfficientNet-B7	84.3%	97.0%	66M	37B
EfficientNet-L2*	85.5%	97.7%	480M	470B

* Noisy Student Training 사용

위 표에서 볼 수 있듯이, EfficientNet-B0는 ResNet-50보다 더 적은 파라미터와 FLOPS로 더 높은 정확도를 달성했습니다. EfficientNet-B7은 ImageNet에서 84.3%의 Top-1 정확도(당시 state-of-the-art)를 달성했지만, 여전히 다른 대형 모델들보다 훨씬 효율적입니다.

EfficientNet의 주요 기여:

• Compound Scaling: 모델의 깊이, 너비, 해상도를 균형 있게 조절하는 새로운 방법론을 제시하여, 모델 크기와 성능 사이의 관계에 대한 이해를 높였습니다.
• 효율적인 모델 설계: AutoML (NAS)를 사용하여 찾은 EfficientNet-B0는, 수동으로 설계된 다른 모델들보다 더 효율적이면서도 강력한 성능을 보여주었습니다.
• 실용성: EfficientNet은 다양한 크기의 모델(B0 ~ B7, L2)을 제공하여, 사용자가 자신의 컴퓨팅 자원과 성능 요구 사항에 맞는 모델을 선택할 수 있게 했습니다.

학계 및 산업계에 미친 영향:

EfficientNet은 모델 경량화 및 효율성에 대한 연구를 촉진했으며, 모바일 기기, 임베디드 시스템 등 자원이 제한된 환경에서 딥러닝 모델을 배포하는 데 널리 사용되고 있습니다. EfficientNet의 compound scaling 아이디어는 다른 모델에도 적용되어, 성능 향상을 가져오기도 했습니다. EfficientNet 이후, EfficientNetV2, MobileNetV3, RegNet 등 효율성을 강조한 후속 연구들이 활발히 진행되었습니다.

한계:

• AutoML(NAS)를 사용하여 찾은 EfficientNet-B0 아키텍처가 왜 다른 아키텍처보다 더 효과적인지에 대한 완전한 이론적 설명은 아직 부족합니다.
• Compound scaling 방법이 모든 종류의 CNN 아키텍처와 태스크에 항상 최적이라고 보장할 수는 없습니다.

그럼에도 불구하고, EfficientNet은 CNN 모델 설계에 대한 새로운 관점을 제시하고, 모델의 효율성을 획기적으로 향상시켰다는 점에서 딥러닝 역사에 중요한 이정표로 평가받고 있습니다.

맺음말

본 장에서는 합성곱 신경망(CNN)의 탄생 배경과 발전 과정, 그리고 ResNet, Inception 모듈, EfficientNet으로 CNN의 가장 중요한 발전을 살펴보았습니다.

CNN은 초기 LeNet-5, AlexNet을 거치며 이미지 인식에서 큰 성과를 보였지만, 깊은 네트워크 학습의 어려움에 직면했습니다. ResNet은 잔차 연결로 이 문제를 해결하여 획기적인 깊이 확장을 가능하게 했습니다. Inception 모듈은 다양한 크기의 필터를 병렬적으로 사용하여 특징 추출의 다양성과 효율성을 높였고, EfficientNet은 모델의 깊이, 너비, 해상도를 균형 있게 조절하는 체계적인 방법을 제시했습니다.

이러한 혁신들은 CNN이 이미지 인식뿐만 아니라 다양한 컴퓨터 비전 태스크에서 핵심적인 역할을 수행하는 데 크게 기여했습니다. 하지만, CNN은 공간적인 지역 패턴(local pattern)을 포착하는 데 강점을 가지는 반면, 순차적인 데이터(sequential data), 특히 자연어(natural language) 처리와 같이 순서와 장거리 의존성(long-range dependency)이 중요한 데이터에는 적합하지 않았습니다.

다음 장에서는 CNN의 컨볼루션 연산과 풀링 연산을 사용하지 않고, Attention 메커니즘만을 사용하여 시퀀스 내 요소 간의 관계를 모델링하는 Transformer 아키텍처를 살펴보겠습니다. Transformer는 자연어 처리 분야에서 획기적인 성능 향상을 가져왔고, 현재는 컴퓨터 비전, 음성 처리 등 다양한 분야로 그 영향력을 확장하고 있습니다. ResNet의 잔차 연결이 CNN의 깊이 한계를 극복했듯, Transformer의 Attention 메커니즘은 시퀀스 데이터 처리의 새로운 지평을 열었습니다.

연습문제

기본 문제

1. 컨볼루션(convolution) 연산이 이미지 처리에서 어떤 역할을 하는지 설명하고, Sobel 필터와 같은 예시를 들어 구체적으로 설명하시오.
2. CNN에서 풀링(pooling) 레이어의 역할과 장점을 설명하고, 최대 풀링(max pooling)과 평균 풀링(average pooling)의 차이점을 비교하시오.
3. ResNet의 핵심 아이디어인 잔차 연결(residual connection)이 깊은 네트워크 학습에 어떻게 도움이 되는지, 기울기 소실/폭주 문제와 관련지어 설명하시오.
4. Inception 모듈의 핵심 아이디어인 “다양한 크기의 필터 사용”과 “1x1 컨볼루션”의 역할을 각각 설명하시오.
5. EfficientNet의 “compound scaling”이 무엇인지 설명하고, 기존의 모델 크기 조절 방법(깊이, 너비, 해상도 중 하나만 조절)과 비교하여 어떤 장점이 있는지 설명하시오.

응용 문제

1. PyTorch를 사용하여 간단한 CNN 모델을 구현하고, MNIST 데이터셋을 사용하여 훈련 및 평가하시오. (데이터 로딩, 모델 정의, 훈련 루프, 평가 루프 포함)
2. ResNet-18 모델을 torchvision.models에서 불러와서 CIFAR-10 데이터셋으로 전이 학습(transfer learning)을 수행하고, 성능을 평가하시오. (데이터 전처리, 모델 로딩, fine-tuning, 평가)
3. expertai_src에 제공된 show_filter_effects 함수를 사용하여, 다양한 필터(blur, sharpen, edge detection 등)가 이미지에 미치는 영향을 시각적으로 비교하고, 각 필터의 특징을 설명하시오.
4. 주어진 ResNet 코드(BasicBlock, Bottleneck)에서 잔차 연결(residual connection)을 제거하고, 동일한 데이터로 훈련했을 때 성능 변화를 측정하고, 그 이유를 분석하시오.
5. SimpleConv2d 클래스를 참고하여, 2D 컨볼루션 연산을 직접 구현하시오. (NumPy 또는 PyTorch의 tensor 연산 사용, torch.nn.Conv2d 사용 금지).

심화 문제

1. 깊은 CNN에서 기울기 소실/폭주 문제가 발생하는 원인을 수학적으로 설명하고, ResNet의 잔차 연결, 배치 정규화, 그리고 Inception 모듈의 1x1 컨볼루션이 각각 이 문제를 어떻게 완화하는지 설명하시오.
2. ResNet, Inception, EfficientNet 논문을 읽고, 각 모델의 핵심 아이디어를 비교 분석하시오. (각 모델의 장단점, 서로 간의 관계, 후속 연구에 미친 영향 등)
3. EfficientNet의 compound scaling 공식을 유도하고 (또는 논문을 참고하여 상세히 설명하고), 주어진 계산 자원 제약 조건 하에서 최적의 모델 크기를 결정하는 방법을 설명하시오.
4. 가우시안 프로세스와 심층 커널 학습(Deep Kernel Learning)의 관계를 설명하고, DKL이 기존의 CNN, GP와 비교하여 어떤 장점을 가지는지 설명하시오.
5. 최근 1-2년 이내에 발표된 CNN 관련 논문 중, ResNet, Inception, EfficientNet의 아이디어를 발전시킨 사례를 1가지 이상 찾아, 그 내용을 요약하고 자신의 견해를 제시하시오. (예: ConvNeXt, NFNet)

클릭하여 내용 보기 (연습문제 해답)

연습문제 해답

기본 문제

1. 컨볼루션 역할 및 Sobel 필터:
   • 역할: 컨볼루션은 이미지와 필터(커널) 간의 연산을 통해 특징을 추출합니다. 필터는 이미지 위를 이동하며 각 위치에서 픽셀 값과 필터 값의 가중합을 계산합니다.
   • Sobel 필터: 이미지의 경계(엣지)를 검출하는 데 사용됩니다. 수직/수평 Sobel 필터는 각각 수직/수평 방향의 밝기 변화를 감지합니다.
2. 풀링 레이어:
   • 역할/장점: 특징 맵의 크기(공간적 차원)를 줄여 계산량을 감소시키고, 이동 불변성(translational invariance)을 높여 과적합을 방지합니다.
   • 최대 풀링 (Max Pooling): 영역 내 최댓값을 선택. 가장 두드러진 특징을 보존합니다.
   • 평균 풀링 (Average Pooling): 영역 내 평균값을 계산. 노이즈에 덜 민감합니다.
3. ResNet 잔차 연결:
   • 잔차 연결: 입력값을 출력에 바로 더하는 “shortcut” 연결입니다. \(H(x) = F(x) + x\)
   • 기울기 소실/폭주 완화: 기울기가 잔차 연결을 통해 직접 전달되므로, 깊은 네트워크에서도 기울기가 잘 전파됩니다. 신경망이 항등 함수(identity mapping, \(F(x) = 0\))를 쉽게 학습할 수 있도록 돕습니다.
4. Inception 모듈:
   • 다양한 크기 필터: 1x1, 3x3, 5x5 등 다양한 크기의 필터를 병렬적으로 사용하여, 이미지 내의 다양한 크기의 특징을 동시에 포착합니다.
   • 1x1 컨볼루션: 채널 간 차원 축소 및 비선형성 추가. 계산량을 줄이면서도 모델의 표현력을 높입니다. (“병목 층” 역할)
5. EfficientNet Compound Scaling:
   • Compound Scaling: 네트워크의 깊이(depth), 너비(width), 해상도(resolution)를 균형 있게 함께 증가시키는 방법입니다. 하나의 계수(compound coefficient)를 사용하여 세 요소를 동시에 조절합니다.
   • 장점: 기존 방법(하나의 요소만 변경)보다 효율적으로 모델 성능을 향상시킵니다. 주어진 계산 자원 제약 조건 하에서 최적의 성능을 달성하도록 모델 크기를 조정할 수 있습니다.

응용 문제

1. CNN 구현 및 MNIST 훈련: (코드 생략) PyTorch를 사용하여 nn.Conv2d, nn.ReLU, nn.MaxPool2d, nn.Linear 등을 조합하여 CNN 모델을 구성하고, DataLoader를 사용하여 MNIST 데이터를 불러와 훈련 및 평가합니다.

2. ResNet-18 전이 학습: (코드 생략) torchvision.models에서 resnet18을 불러와 마지막 층(fully connected layer)을 CIFAR-100에 맞게 교체하고, 일부 층을 fine-tuning합니다.

3. show_filter_effects 분석: (코드 생략) show_filter_effects 함수는 주어진 이미지에 다양한 필터(Gaussian Blur, Sharpen, Edge Detection, Emboss, Sobel X)를 적용하고 그 결과를 시각화합니다. 각 필터는 이미지의 특정 특징(흐림, 선명하게, 경계 검출 등)을 강조하거나 변형합니다.

4. ResNet 잔차 연결 제거: (코드 생략) 잔차 연결을 제거하면 기울기 소실/폭주 문제로 인해 깊은 네트워크의 학습이 어려워지고, 성능이 저하되는 경향을 보입니다.

5. 2D 컨볼루션 직접 구현: (코드 생략) 중첩된 for 루프를 사용하여 입력 텐서의 각 위치에서 커널과의 요소별 곱셈 및 합산을 수행합니다. im2col과 같은 기법을 사용하여 행렬 곱셈으로 변환하면 더 효율적입니다.

심화 문제

1. 기울기 소실/폭주:

   • 원인: 역전파 시 기울기가 연쇄 법칙(chain rule)에 따라 반복적으로 곱해지면서, 깊은 층으로 갈수록 기울기가 매우 작아지거나(vanishing) 커지는(exploding) 현상입니다. 활성화 함수의 미분 값이 1보다 작으면 (ex: sigmoid, tanh) 소실, 1보다 크면 폭주가 발생하기 쉽습니다.
   • ResNet 잔차 연결: 기울기가 잔차 연결을 통해 직접 전달되므로, 기울기 소실/폭주 문제를 완화합니다.
   • 배치 정규화: 각 층의 입력을 정규화하여 활성화 함수의 입력이 적절한 범위에 있도록 유지하므로 기울기 소실/폭주를 줄여줍니다.
   • Inception 1x1 컨볼루션: 채널 수를 줄여 계산량을 감소시키고, 기울기 소실/폭주를 간접적으로 완화합니다. (파라미터 수가 줄어들기 때문)

2. ResNet, Inception, EfficientNet 비교: (상세 비교 생략)

   • ResNet: 잔차 연결을 통해 깊은 네트워크 학습을 가능하게 함.
   • Inception: 다양한 크기의 필터를 병렬적으로 사용하여 다양한 스케일의 특징을 추출. 1x1 컨볼루션을 사용하여 계산 효율성을 높임.
   • EfficientNet: Compound Scaling을 통해 모델의 깊이, 너비, 해상도를 균형 있게 조절하여 효율성과 성능을 모두 향상시킴.

3. EfficientNet Compound Scaling: (공식 유도/상세 설명 생략) compound coefficient (Φ)를 사용하여 깊이(α^Φ), 너비(β^Φ), 해상도(γ^Φ)를 조절. α, β, γ는 작은 그리드 탐색으로 찾은 상수. 제약 조건: α ⋅ β² ⋅ γ² ≈ 2.

4. 가우시안 프로세스(GP)와 DKL:

   • GP: 함수에 대한 확률 분포. 커널 함수를 사용하여 함수 값들 사이의 공분산을 정의. 베이지안 추론을 통해 예측의 불확실성 제공.
   • DKL (Deep Kernel Learning): 딥러닝(신경망)을 사용하여 데이터로부터 특징을 추출하고, 이 특징을 GP의 커널 함수의 입력으로 사용. 딥러닝의 표현 학습 능력과 GP의 불확실성 추정 능력을 결합.
   • 장점: 데이터 효율성, 불확실성 추정, 유연한 특징 표현.
   • 단점: GP의 계산 복잡도가 여전히 존재.

5. 최신 CNN 논문: (예시: ConvNeXt, NFNet 등. 논문 요약 및 견해 생략)

참고 자료

1. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex (Hubel & Wiesel, 1962): 고양이 시각 피질 연구. CNN의 receptive field 개념에 영감을 준 논문. (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1359523/)
2. The Scientist and Engineer’s Guide to Digital Signal Processing (Steven W. Smith): 디지털 신호 처리의 기본 원리를 설명하는 책. 컨볼루션, 필터 등을 이해하는 데 도움이 됩니다. (http://www.dspguide.com/pdfbook.htm)
3. Gradient-based learning applied to document recognition (LeCun et al., 1998): CNN을 이용한 문자 인식. LeNet-5 소개. (http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf)
4. Deep Residual Learning for Image Recognition (He et al., 2015): ResNet 원 논문. (https://arxiv.org/pdf/1512.03385.pdf)
5. Network in Network (Lin et al., 2013): 1x1 컨볼루션의 아이디어를 제시한 논문. (https://arxiv.org/pdf/1312.4400.pdf)
6. Very Deep Convolutional Networks for Large-Scale Image Recognition (Simonyan & Zisserman, 2014): VGGNet 논문. (https://arxiv.org/pdf/1409.1557.pdf)
7. Dive into Deep Learning (Zhang et al., 2023): 9장 “Convolutional Neural Networks”에서 CNN의 기본 개념과 ResNet을 설명. (https://d2l.ai/chapter_convolutional-neural-networks/index.html)
8. CS231n: Convolutional Neural Networks for Visual Recognition (Stanford University): CNN 강의 자료. (http://cs231n.github.io/convolutional-networks/)
9. Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift (Li et al., 2018): 배치 정규화와 드롭아웃을 함께 사용할 때 주의할 점을 설명하는 논문.
10. Rethinking the Inception Architecture for Computer Vision (Szegedy et al., 2015): Inception-v3, 인셉션 모듈에 대한 설명 (https://arxiv.org/abs/1512.00567)